
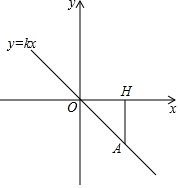
 已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.分析 (1)由点A的纵坐标、点A所在的象限结合△AOH的面积为3,可求出点A的坐标,再根据点A的坐标利用待定系数法,可求出正比例函数的表达式;
(2)设点P的坐标为(a,0),根据△AOP的面积为5,即可得出关于a的含绝对值符号的一元一次方程,解之即可得出结论.
解答 解:(1)∵点A在第四象限,点A的横坐标为3,且△AOH的面积为3.
∴点A的纵坐标为-2,
∴点A的坐标为(3,-2).
将点A(3,-2)代入y=kx,
-2=3k,解得:k=-$\frac{2}{3}$,
∴正比例函数的表达式为y=-$\frac{2}{3}$x.
(2)设点P的坐标为(a,0),
则S△AOP=$\frac{1}{2}$|a|×|-2|=5,
解得:a=±5,
∴在x轴上能找到一点P,使△AOP的面积为5,此时点P的坐标为(-5,0)或(5,0).
点评 本题考查了待定系数法求正比例函数解析式以及三角形的面积,解题的关键是:(1)根据三角形的面积找出点A的坐标;(2)利用三角形的面积找出关于a的含绝对值符号的一元一次方程.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:填空题
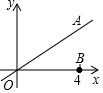 如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.
如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
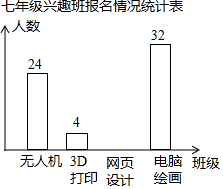 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.| 兴趣班名称 | 频率 |
| “无人机” | a |
| “3D打印” | b |
| “网页设计” | 0.25 |
| “电脑绘画” | 0.4 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A类 | 50 | 20 |
| B类 | 150 | 15 |
| C类 | 300 | 10 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com