
【题目】如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=![]() (∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
其中正确的是( )

A. ①②③ B. ①③④ C. ①②④ D. ①②③④
【答案】D
【解析】
①根据BD垂直FD,FH⊥BE和∠FGD=∠BGO,证明结论正确;
②根据角平分线的定义和三角形外角的性质证明结论正确;
③证明∠DBE=∠BAC-∠C-∠DBE,根据①的结论,证明结论正确;
④根据角平分线的定义和三角形外角的性质证明结论正确.
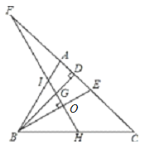
①由题意可知,∠FDG=∠BOG=90°,
∵∠FGD=∠BGO,
∴∠DBE=∠F,故①正确;
②∵∠BAF=∠ABC+∠C=2∠EBC+∠C,
∴∠BAF+∠C=2(∠EBC+∠C)=2∠BEF,故②正确;
③∵∠ABD=90°-∠BAC,
∴∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC=∠CBD-∠DBE-90°+∠BAC,
∵∠CBD=90°-∠C,
∴∠DBE=∠BAC-∠C-∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC-∠C-∠F,
∴∠F=![]() (∠BAC﹣∠C),故③正确;
(∠BAC﹣∠C),故③正确;
④∵∠AEB=∠EBC+∠C,∠EBC =∠ABE,
∴∠AEB=∠ABE+∠C,
又∵BD⊥FC,∠DBE=∠F,
∴∠FGD=∠FEB,
∴∠BGH=∠FGD=∠FEB=∠ABE+∠C,故④正确;
故正确的是①②③④.
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某闭合电路中,其两端电压恒定,电流I(A)与电阻R(Ω)图象如图所示,回答问题: 
(1)写出电流I与电阻R之间的函数解析式.
(2)如果一个用电器的电阻为5Ω,其允许通过的最大电流是1A,那么这个用电器接在这个闭合电路中,会不会烧毁?说明理由.
(3)若允许的电流不超过4A时,那么电阻R的取值应该控制在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是( )
A. 3分钟 B. 4分钟 C. 5分钟 D. 6分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个点,分别对应的数为a,b,c,d,且满足a,b是方程|x+7|=1的两个解(a<b),且(c﹣12)2与|d﹣16|互为相反数.
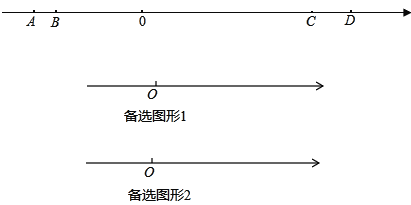
(1)填空:a= 、b= 、c= 、d= ;
(2)若线段AB以3个单位/秒的速度向右匀速运动,同时线段CD以1单位长度/秒向左匀速运动,并设运动时间为t秒,A、B两点都运动在CD上(不与C,D两个端点重合),若BD=2AC,求t得值;
(3)在(2)的条件下,线段AB,线段CD继续运动,当点B运动到点D的右侧时,问是否存在时间t,使BC=3AD?若存在,求t得值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
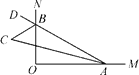
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com