
 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据图象分别判断即可,行驶的最远距离是120千米,共行驶240千米,共用时间是4.5小时.
解答 解:①行驶的最远距离是120千米,共行驶240千米,故此选项错误;
②根据图象从1.5时到2时,是停留时间,停留0.5小时,故此选项正确;
③汽车在整个行驶过程中的平均速度为$\frac{240}{4.5}=\frac{160}{3}$千米/时,故此选项错误;
④汽车自出发后3小时至4.5小时之间路程与时间成一次函数关系,因而速度不变,故此选项错误,
故正确的说法是:②.
故选:D.
点评 此题主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
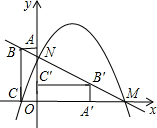 如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题:
如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 成本(元) | 50 | 35 |
| 利润(元) | 20 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com