
分析 (1)设A的十位数字为a,个位数字为b,其“诚勤数”为100a+20+b、“立达数”为10a+b+2,作差整理即可得;
(2)设B=10a+b,1≤a≤9,0≤b≤9(B加上2后各数字之和变小,说明个位发生了进位),根据““立达数”的各位数字之和是B的各位数字之和的一半”列出关于a、b的方程,求解可得.
解答 解:(1)设A的十位数字为a,个位数字为b,
则A=10a+b,它的“诚勤数”为100a+20+b,它的“立达数”为10a+b+2,
∴100a+20+b-(10a+b+2)=90a+18=6(15a+3),
∵a为整数,
∴15a+3是整数,
则“诚勤数”与“立达数”之差能被6整除;
(2)设B=10a+b,1≤a≤9,0≤b≤9(B加上2后各数字之和变小,说明个位发生了进位),
∴B+2=10a+b+2,
则B的“立达数”为10(a+1)+(b+2-10),
∴a+1+b+2-10=$\frac{1}{2}$(a+b),
整理,得:a+b=14,
∵1≤a≤9,0≤b≤9,
∴$\left\{\begin{array}{l}{a=8}\\{b=6}\end{array}\right.$、$\left\{\begin{array}{l}{a=6}\\{b=8}\end{array}\right.$、$\left\{\begin{array}{l}{a=9}\\{b=5}\end{array}\right.$、$\left\{\begin{array}{l}{a=5}\\{b=9}\end{array}\right.$,
经检验:86和95不符合题意,舍去,
∴所求两位数为68或59.
点评 本题主要考查因式分解的应用,根据题意表示出A、B两数的“立达数”、“诚勤数”及其变化是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
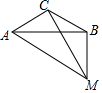 如图,在△ABC中,∠ACB=120°,点M为△ABC外一点,且∠AMB=60°,若CM平分∠AMB.求证:AM+BM=$\sqrt{3}$CM.
如图,在△ABC中,∠ACB=120°,点M为△ABC外一点,且∠AMB=60°,若CM平分∠AMB.求证:AM+BM=$\sqrt{3}$CM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
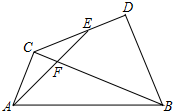 如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,以BC为斜边向外作等腰Rt△DBC,E为CD的中点,AE交BC于F,则EF的长度为$\frac{\sqrt{10}}{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,以BC为斜边向外作等腰Rt△DBC,E为CD的中点,AE交BC于F,则EF的长度为$\frac{\sqrt{10}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com