
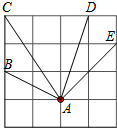
 如图,在4×4的网格图中,小正方形的边长为1,则图中用字母表示的四条线段中长度为$\sqrt{10}$的线段是AD.
如图,在4×4的网格图中,小正方形的边长为1,则图中用字母表示的四条线段中长度为$\sqrt{10}$的线段是AD.  口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{m+1}{m-1}$ | D. | $\frac{m+1}{1-m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 看图填空:
看图填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
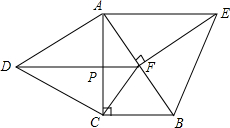 如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.
如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 交通方式 | 频数(人数) | 频率 |
| 公共汽车 | m | 0.25 |
| 小车 | 24 | 0.20 |
| 摩托车 | 36 | n |
| 自行车 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图矩形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).
如图矩形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3+6ab2-5a2 | B. | a3-6ab2-5a2 | C. | a3-5a2 | D. | a2+6ab-5a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-7}$ | B. | $\root{3}{2m}$ | C. | $\sqrt{{x^2}+1}$ | D. | $\root{3}{{\frac{a}{b}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com