
分析 (1)根据题意即可得到结论;
(2)8分钟进24吨,则每分钟进3吨,则当0≤t≤8时,Q=3t;由于进油管和出油管同时打开24分钟,油罐内的油从24吨增至40吨,每分钟进$\frac{2}{3}$吨,所以当8≤t≤24时,Q=$\frac{2}{3}$t+$\frac{56}{3}$;由于出油管的速度为每分钟出油$\frac{7}{3}$吨,则40吨需$\frac{288}{\;}$分钟,则24≤t≤$\frac{288}{7}$时,Q=-$\frac{7}{3}$t+$\frac{199}{3}$.
解答 解:(1)进油管每分钟进油为$\frac{24}{8}$=3吨/分钟;出油管每分钟出油为$\frac{24×3-40+24}{24}$=$\frac{7}{3}$吨/分钟;
(2)解:(1)当0≤t≤8时,Q=$\frac{24}{3}$t=3t;
当8≤t≤24时,Q=24+$\frac{40-24}{24}$(t-8)=$\frac{2}{3}$t+$\frac{56}{3}$;
当24≤t≤$\frac{288}{7}$时,Q=40-$\frac{7}{3}$(t-24)=-$\frac{7}{3}$t+$\frac{199}{3}$.
点评 本题考查了一次函数的应用:分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
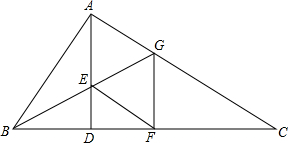 如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.
如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 商品价格 购物金额 | 120 | 180 | 200 | 260 |
| 甲商场 | 96 | 144 | 160 | 208 |
| 乙商场 | 120 | 200 | 200 | ,242 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 册数(x) | 1 | 2 | 3 | … | |
| 价格(y) | 7.5 | 15 | 30 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
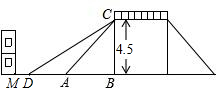 如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)
如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com