
【题目】在△ABC中,![]() ,BE是AC边上的中线,点D在射线BC上.
,BE是AC边上的中线,点D在射线BC上.
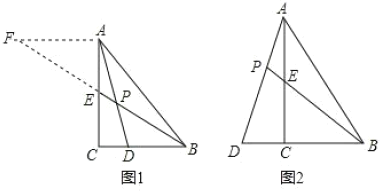
(1)如图1,点D在BC边上,![]() ,AD与BE相交于点P,过点A作
,AD与BE相交于点P,过点A作![]() ,交BE的延长线于点F,易得
,交BE的延长线于点F,易得![]() 的值为 ;
的值为 ;
(2)如图2,在△ABC中,![]() ,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,
,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若CD=2,AC=6,则BP= .
【答案】(1)![]() ;(2)
;(2)![]() ;(3)6
;(3)6
【解析】
(1)易证△AEF≌△CEB,则有AF=BC.设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,然后根据相似三角形的性质就可求出![]() 的值;(2)过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.易证△AEF≌△CEB,则有EF=BE,AF=BC=2k.易证△AFP∽△DBP,然后根据相似三角形的性质就可求出
的值;(2)过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.易证△AEF≌△CEB,则有EF=BE,AF=BC=2k.易证△AFP∽△DBP,然后根据相似三角形的性质就可求出![]() 的值;
的值;
(3)当CD=2时,可依次求出BC、AC、EC、EB、EF、BF的值,然后根据![]() 的值求出
的值求出![]() 的值,就可求出BP的值.
的值,就可求出BP的值.
解:(1)如图1中,
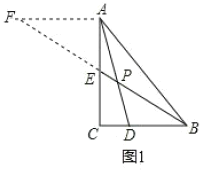
∵AF∥BC,
∴∠F=∠EBC,
∵∠AEF=∠BEC,AE=EC,
∴△AEF≌△CEB(AAS),
∴AF=BC.
设CD=k,则DB=2k,AF=BC=3k,
∵AF∥BC,
∴△APF∽△DPB,
∴![]() ,
,
故答案是:![]() ;
;
(2)如图2,过点A作AF∥DB,交BE的延长线于点F,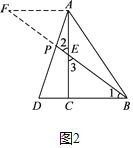
设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠1.
在△AEF和△CEB中,
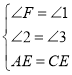 ,
,
∴△AEF≌△CEB,
∴EF=BE,AF=BC=2k.
∵AF∥DB,
∴△AFP∽△DBP,
∴![]() ;
;
(3)当CD=2时,BC=4,
∵AC=6,
∴EC=AE=3,
∴EB= ![]()
∴EF=BE=5,BF=10.
∵![]() ,
,
![]() ,
,
∴BP=![]() BF=
BF=![]() ×10=6.
×10=6.
故答案为6.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
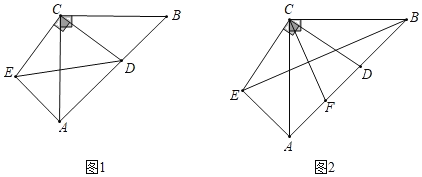
【题目】如图1.在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.
(1)连接ED,若CD=3,AE=4,求AB的长;
(2)如图2,若点F为AD的中点,连接EB、CF,求证:CF⊥EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
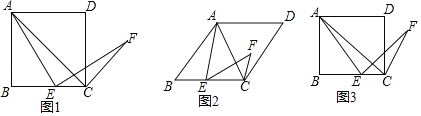
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法.下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.问题情境:在四边形ABCD中,AC是对角线,E为边BC上一点,连接AE.以E为旋转中心,将线段AE顺时针旋转,旋转角与∠B相等,得到线段EF,连接CF.
(1)特例如图1,若四边形ABCD是正方形,求证:AC⊥CF;
(2)拓展分析一:如图2,若四边形ABCD是菱形,探究下列问题:
①当∠B=50°时,求∠ACF的度数;
②针对图2的条件,写出一般的结论(不必证明);
(3)拓展探究二:如图3,若四边形ABCD是矩形,且BC=kAB(k>1).若前提条件不变,特例分析中得到的结论还成立吗?若成立,请证明;若不成立,修改题中的条件使结论成立(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨某中学学校为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类).根据图中提供的信息,解答下面的问题:

(1)在这次调查中,参与问卷调查的学生共有多少名学生?
(2)通过计算补全条形统计图;
(3)若学校有900名学生,估计喜欢篮球和足球的学生共有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知![]() ,
,![]() ,矩形OABC的对角线交于点P,点M在经过点P的函数
,矩形OABC的对角线交于点P,点M在经过点P的函数![]() 的图象上运动,k的值为__________,OM长的最小值__________.
的图象上运动,k的值为__________,OM长的最小值__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y=x2﹣3x﹣4与x轴交于A,B两点(点A在点B的右侧),有点C(﹣2,6).
(1)求A,B两点的坐标.
(2)若点D(1,﹣3),点E在线段OA上,且∠ACB=∠ADE,延长ED交y轴于点F,求△EFO的面积.
(3)若M在直线AC上,点Q在抛物线上,是否存在点M和点N,使以Q,M,N,A为顶点的四边形是正方形?若存在,直接写出M点的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
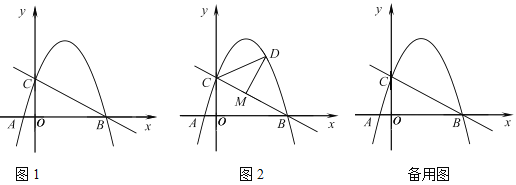
(1)求抛物线的解析式;
(2)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请求出点
是等腰三角形,请求出点![]() 的坐标;
的坐标;
(3)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一个动点.过点
上方抛物线上的一个动点.过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,请求出点
的2倍?若存在,请求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
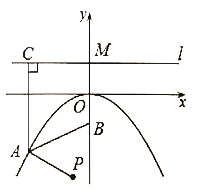
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com