
分析 (1)设抛物线解析式为顶点式方程,然后将点D、B的坐标代入来求系数的值,从而得到该抛物线的解析式;
(2)设P(x,y),过点P作PF⊥y轴于点F.根据点的坐标与图形的性质得到相关线段的长度:OE=2,OC=5,PF=-x,OF=-y,利用三角形的面积公式、二次函数图象上点的坐标特征列出S关于x的二次函数,利用二次函数最值的求法得到点P的坐标;
(3)分三种情况进行讨论:
①当点Q位于AE的中垂线与AC的交点处时,△AEQ是等腰三角形;
②当AE=QE时,△AEQ是等腰三角形,Q点位于AC与抛物线对称轴的交点处;
③当AE=AQ时,△AEQ是等腰三角形,过点Q作QG⊥y轴于点G,通过解直角三角形来求线段OG的长度,从而得到点Q的坐标.
解答 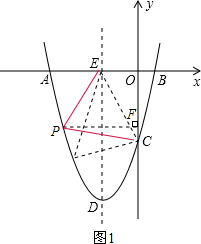 解:(1)设该抛物线的解析式为y=a(x-h)2+k,将顶点坐标(-2,-9)代入得:
解:(1)设该抛物线的解析式为y=a(x-h)2+k,将顶点坐标(-2,-9)代入得:
y=a(x+2)2-9.
把B(1,0)代入得:9a-9=0,a=1.
所以,该抛物线的解析式为y=(x+2)2-9,化为一般式为:y=x2+4x-5;
(2)设P(x,y),如图1,过点P作PF⊥y轴于点F.
∵E(-2,0),C(0,-5),
∴OE=2,OC=5,PF=-x,OF=-y.
设△PCE的面积为S,则
S=-$\frac{1}{2}$x(-y+5)+$\frac{1}{2}$y(-x-2)-$\frac{1}{2}$×2×5=-$\frac{5}{2}$x-y-5.
∵y=x2+4x-5,
∴S=-x2-$\frac{13}{2}$x.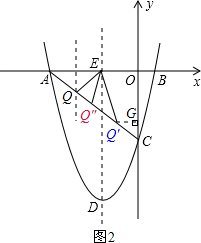
当x=-$\frac{13}{4}$时,S最大,此时y=(-$\frac{13}{4}$)2+4×(-$\frac{13}{4}$)-5=-$\frac{119}{16}$,
∴当△PCE的面积最大时,P(-$\frac{13}{4}$,-$\frac{119}{16}$);
(3)Q点存在,共有3个.
∵A(-5,0),C(0,-5),E(-2,0),
∴△AOC是等腰直角三角形,∠EAC=45°.
设直线AC的解析式为y=kx+b(k≠0).易得直线AC的解析式为y=-x-5.
①当点Q位于AE的中垂线与AC的交点处时,△AEQ是等腰三角形,Q点的横坐标为-3.5,Q(-3.5,-1.5);
②当AE=QE时,△AEQ是等腰三角形,Q点位于AC与抛物线对称轴的交点处,Q(-2,-3);
③当AE=AQ时,△AEQ是等腰三角形,过点Q作QG⊥y轴于点G,易得QG=$\frac{3\sqrt{2}}{2}$,则Q($\frac{3\sqrt{2}}{2}$-5,-$\frac{3\sqrt{2}}{2}$).
点评 本题考查了二次函数综合题.其中涉及到了待定系数法求二次函数的解析式,二次函数的最值的求法,三角形的面积公式,等腰三角形的判定与性质.解答(3)题时,要分类讨论,以防漏解,该题综合性比较强,难度较大.


科目:初中数学 来源: 题型:解答题
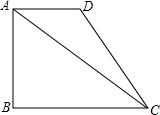 如图,在梯形ABCD中,AD∥BC,AB⊥BC,已知AD=2,cot∠ACB=$\frac{4}{3}$,梯形ABCD的面积是9;
如图,在梯形ABCD中,AD∥BC,AB⊥BC,已知AD=2,cot∠ACB=$\frac{4}{3}$,梯形ABCD的面积是9;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)
已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
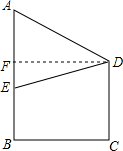 如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米).
如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
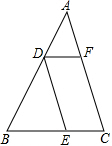 如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上,已知:DE∥AC,DF∥BC.
如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上,已知:DE∥AC,DF∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,P为AB上一点,则下列四个条件中
如图,在△ABC中,P为AB上一点,则下列四个条件中查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com