
| 1 | 2 | 3 | 4 | 5 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
分析 (1)根据1~5这5个自然数中,每次取两个不同的数相同方法列式计算可得;
(2)根据1~6这6个自然数中,每次取两个不同的数相同方法列式计算可得;
(3)n为奇数时可类比在1~5这5个自然数中,每次取两个不同的数相同方法列式化简可得;
(4)n为偶数时可类比在1~6这6个自然数中,每次取两个不同的数相同方法列式化简可得;
(5)根据三角形三边关系,即两边之和大于第三边,两边之差小于第三边,则各边长都是整数,最大边长为51的三角形的个数是n为奇数时的取法再加上两边相等的$\frac{n+1}{2}$种取法,列式计算可得.
解答 解:(1)在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有$\frac{1+2+3+4+5+6+7-\frac{7+1}{2}}{2}$=12种不同取法;
(2)在1~8这8个自然数中,每次取两个不同的数,使得所取的两个数之和大于8,共有$\frac{1+2+3+4+5+6+7+8-\frac{8}{2}}{2}$=16种不同取法;
(3)在1~n(n为奇数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{1+2+3+…+n-\frac{n+1}{2}}{2}$=$\frac{{n}^{2}-1}{4}$种不同取法;
(4)在1~n(n为偶数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{1+2+3+…+n-\frac{n}{2}}{2}$=$\frac{{n}^{2}}{4}$种不同取法;
(5)根据三角形三边关系,即相当于在1~51这51个自然数中,每次取两个不同的数,使得所取的两个数之和大于51,
共有$\frac{5{1}^{2}-1}{4}$+$\frac{51+1}{2}$=676种不同取法,
故各边长都是整数,最大边长为51的三角形有676个.
故答案为:(1)12;(2)16;(3)$\frac{{n}^{2}-1}{4}$;(4)$\frac{{n}^{2}}{4}$.
点评 此题考查了一道数字规律的问题和三角形的三边关系,能够从特殊推广到一般.


科目:初中数学 来源: 题型:选择题
| A. | (x+5)(y-5)=x-25 | B. | (x+y)2(x-y)2=x4-2x2y2+y4 | ||
| C. | 6m3÷(-3m2)•(2m)2=4m3 | D. | (8x3-4x2-2x)÷(-2x)=-4x2+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+y是整式 | B. | 多项式-3a2b+7a2b2+1的次数是3 | ||
| C. | 单项式$-\frac{2}{3}{a^2}b$的系数为-2 | D. | $\frac{1}{a}$和0都是单项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
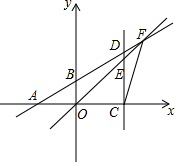 如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.
如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{8}$=±2 | C. | (-$\sqrt{2}$)4=-4 | D. | ($\root{5}{-8}$)5=-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2-1=-2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x-2}$有意义的x的取值范围是x<2 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{-10}$ | C. | $\sqrt{a+1}$ | D. | $\sqrt{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$=±5 | B. | $\sqrt{-16}$=4 | C. | $\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$ | D. | $\sqrt{9}$=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com