

分析 (1)由题意补全图形即可;
(2)利用对称的性质计算出∠DAP,再利用等边三角形的性质,利用三角形的内角和计算即可;
(3)先判断出,点B,C,D,在以A为圆心的圆上,再利用圆周角的特点计算即可.
解答 解:(1)补全图形,如图1所示,
(2)∵点B关于直线AP的对称点为D,
∴∠DAP=∠BAP=15°,AD=AC
∴∠DAB=30°,
∵∠BAC=60°,
∴∠DAC=90°,
∴β=∠ACE=∠ADE=45°,
∵∠BAP=15°,∠BAC=60°,
∴γ=∠AEC=180°-(∠BAP+∠BAC)-∠ACE=60°;
(3)①α=β+60°;
理由如下: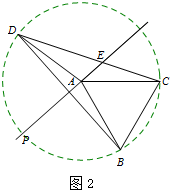
∵点D与点B关于直线AP对称,
∴AD=AB,∠PAD=∠PAB=α,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴AD=AB=AC,
∴点B,C,D,在以A为圆心的圆上,
∴∠BAD=2∠BCD,
∵∠BAD=∠PAD+∠PAB=2α,
∠BCD=∠ACE+∠BCA=β+60°,
∴2α=2(β+60°),
∴α=β+60°;
②由②知,∠PAB=∠BCD,
∴A,B,C,E四点共圆,
∴∠AEC+∠ABC=180°,
∵△ABC为等边三角形,
∴∠ABC=60°,
∴∠AEC=180°-∠ABC=120°
∴γ=∠AEC=120°.
点评 此题是三角形综合题,主要考查了对称的性质,三角形的内角和定理,等边三角形的性质圆周角的性质,得到点B,C,D,在以A为圆心的圆上作出辅助线是解本题的关键,判断A,B,C,E四点共圆是本题的难点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
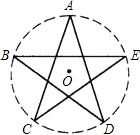 如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )| A. | a•sin72° | B. | $\frac{a}{tan72°}$ | C. | $\frac{a}{cos18°}$ | D. | $\frac{a}{cos36°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
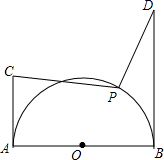 如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.
如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com