
【题目】已知锐角∠MBN的余弦值为![]() ,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、E.点F在线段BE上(点F不与点B重合),且∠EAF=∠MBN.
,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、E.点F在线段BE上(点F不与点B重合),且∠EAF=∠MBN.
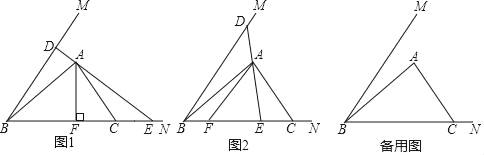
(1)如图1,当AF⊥BN时,求EF的长;
(2)如图2,当点E在线段BC上时,设BF=x,BD=y,求y关于x的函数解析式并写出函数定义域;
(3)联结DF,当△ADF与△ACE相似时,请直接写出BD的长.
【答案】(1)16(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)由锐角三角函数可求AC=15,根据勾股定理和三角形面积公式可求AB,AF的长,即可求EF的长;
(2)通过证△FAE∽△FCA和△BDE∽△CFA,可得y关于x的函数解析式;
(3)分△ADF∽△CEA,△ADF∽△CAE两种情况讨论,通过等腰三角形的性质和相似三角形性质可求BD的长.
(1)∵在Rt△ABC中,∠BAC=90°,
∴cos∠BCA=cos∠MBN=![]() ,
,
∴![]()
∴AC=15
∴AB=![]() =20
=20
∵S△ABC=![]() ×AB×AC=
×AB×AC=![]() ×BC×AF,
×BC×AF,
∴AF=![]() =12,
=12,
∵AF⊥BC
∴cos∠EAF=cos∠MBN=![]()
∴AE=20
∴EF=![]() =16
=16
(2)如图,过点A作AH⊥BC于点H,
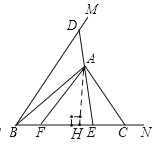
由(1)可知:AB=20,AH=12,AC=15,
∴BH=![]() =16,
=16,
∵BF=x,
∴FH=16﹣x,CF=25﹣x,
∴AF2=AH2+FH2=144+(16﹣x)2=x2﹣32x+400,
∵∠EAF=∠MBN,∠BCA=∠MBN
∴∠EAF=∠BCA,且∠AFC=∠AFC,
∴△FAE∽△FCA
∴![]() ,∠AEF=∠FAC,
,∠AEF=∠FAC,
∴AF2=FC×EF
∴x2﹣32x+400=(25﹣x)×EF,
∴EF=![]()
∴BE=BF+EF=![]()
∵∠MBN=∠ACB,∠AEF=∠FAC,
∴△BDE∽△CFA
∴![]()
∴![]()
∴y=![]() (0<x≤
(0<x≤![]() )
)
(3)如图,若△ADF∽△CEA,
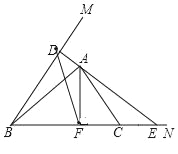
∵△△ADF∽△CEA,
∴∠ADF=∠AEC,
∵∠EAF=∠MBN,∠EAF+∠DAF=180°,
∴∠DAF+∠MBN=180°,
∴点A,点F,点B,点D四点共圆,
∴∠ADF=∠ABF,
∴∠ADF=∠AEC=∠ABF,
∴AB=AE,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,且∠ABF=∠AEC,∠ACB=∠MBN=∠EAF,
∴∠AEC+∠EAF=90°,∠AEC+∠MBN=90°,
∴∠BDE=90°=∠AFC,
∵S△ABC=![]() ×AB×AC=
×AB×AC=![]() ×BC×AF,
×BC×AF,
∴AF=![]() =12,
=12,
∴BF=![]() ,
,
∵AB=AE,∠AFC=90°,
∴BE=2BF=32,
∴cos∠MBN=![]() ,
,
∴BE=![]() ,
,
如图,若△ADF∽△CAE,
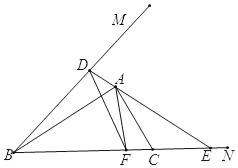
∵△ADF∽△CAE,
∴∠ADF=∠CAE,∠AFD=∠AEC,
∴AC∥DF
∴∠DFB=∠ACB,且∠ACB=∠MBN,
∴∠MBN=∠DFB,
∴DF=BD,
∵∠EAF=∠MBN,∠EAF+∠DAF=180°,
∴∠DAF+∠MBN=180°,
∴点A,点F,点B,点D四点共圆,
∴∠ADF=∠ABF,
∴∠CAE=∠ABF,且∠AEC=∠AEC,
∴△ABE∽△CAE
∴![]()
设CE=3k,AE=4k,(k≠0)
∴BE=![]() k,
k,
∵BC=BE﹣CE=25
∴k=![]()
∴AE=![]() ,CE=
,CE=![]() ,BE=
,BE=![]()
∵∠ACB=∠FAE,∠AFC=∠AFE,
∴△AFC∽△EFA,
∴![]() ,
,
设AF=7a,EF=20a,
∴CF=![]() a,
a,
∵CE=EF﹣CF=![]() a=
a=![]() ,
,
∴a=![]() ,
,
∴EF=![]() ,
,
∵AC∥DF,
∴![]() ,
,
∴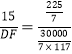 ,
,
∴DF=![]() ,
,
综上所述:当BD为![]() 或
或![]() 时,△ADF与△ACE相似
时,△ADF与△ACE相似


科目:初中数学 来源: 题型:
【题目】一块长和宽分别为40厘米和25厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体纸盒,使它的底面积为450平方厘米.那么纸盒的高是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
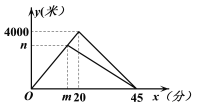
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
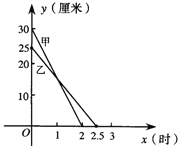
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽甲所用的时间为 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡低?
查看答案和解析>>
科目:初中数学 来源: 题型:
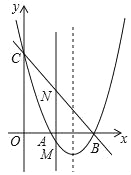
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线上在x轴下方的动点,过M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)E是抛物线对称轴上一点,F是抛物线上一点,是否存在以A,B,E,F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
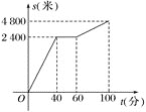
A. 小明中途休息用了20分钟 B. 小明休息前爬山的速度为每分钟60米
C. 小明在上述过程中所走路程为7 200米 D. 小明休息前后爬山的平均速度相等
查看答案和解析>>
科目:初中数学 来源: 题型:
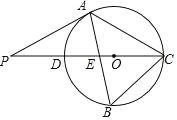
【题目】如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P.
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径;
,求⊙O的直径;
(3)在(2)的条件下,若点B等分半圆CD,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com