
【题目】如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD. 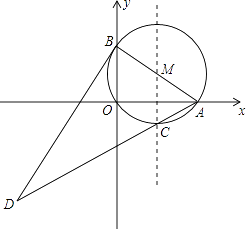
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.
【答案】
(1)解:∵由题意可得出:OA2+OB2=AB2,AO=4,BO=3,
∴AB=5,
∴圆的半径为 ![]()
(2)证明:由题意可得出:M(2, ![]() )
)
又∵C为劣弧AO的中点,由垂径定理且 MC= ![]() ,故 C(2,﹣1)
,故 C(2,﹣1)
过 D 作 DH⊥x 轴于 H,设 MC 与 x 轴交于 K,
则△ACK∽△ADH,
又∵DC=4AC,
故 DH=5KC=5,HA=5KA=10,
∴D(﹣6,﹣5)
设直线AB表达式为:y=kx+b,
![]() ,
,
解得: 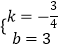
故直线AB表达式为:y=﹣ ![]() x+3,
x+3,
同理可得:根据B,D两点求出BD的表达式为y= ![]() x+3,
x+3,
∵kAB×kBD=﹣1,
∴BD⊥AB,BD为⊙M的切线
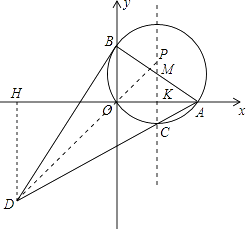
(3)解:取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,
此P点为所求,且线段DO的长为|DP﹣AP|的最大值;
设直线DO表达式为 y=kx,
∴﹣5=﹣6k,
解得:k= ![]() ,
,
∴直线DO表达式为 y= ![]() x
x
又∵在直线DO上的点P的横坐标为2,y= ![]() ,
,
∴P(2, ![]() ),
),
此时|DP﹣AP|=DO= ![]() =
= ![]()
【解析】(1)利用A,B点坐标得出AO,BO的长,进而得出AB的长,即可得出圆的半径;(2)根据A,B 两点求出直线AB表达式为:y=﹣ ![]() x+3,根据 B,D 两点求出 BD 表达式为 y=
x+3,根据 B,D 两点求出 BD 表达式为 y= ![]() x+3,进而得出BD⊥AB,求出BD为⊙M的切线;(3)根据D,O两点求出直线DO表达式为 y=
x+3,进而得出BD⊥AB,求出BD为⊙M的切线;(3)根据D,O两点求出直线DO表达式为 y= ![]() x 又在直线 DO 上的点P的横坐标为2,所以 p(2,
x 又在直线 DO 上的点P的横坐标为2,所以 p(2, ![]() ),此时|DP﹣AP|=DO=
),此时|DP﹣AP|=DO= ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0). 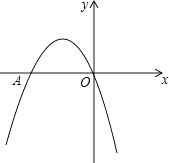
(1)求此二次函数的解析式;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点. 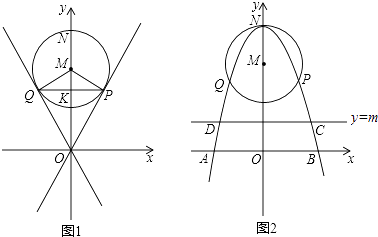
(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).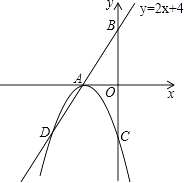
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).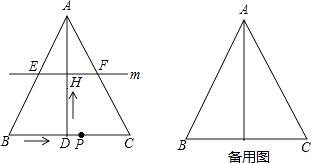
(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是30cm幻灯片到屏幕的距离是1.5m,幻灯片上小树的高度是10cm,则屏幕上小树的高度是( )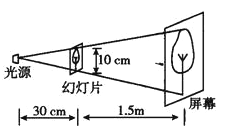
A.50cm
B.500cm
C.60 cm
D.600cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com