
分析 利用勾股定理可得x的值,再利用“夹逼法”估算即可.
解答 解:(1)由勾股定理得:x=$\sqrt{{9}^{2}{+5}^{2}}$=$\sqrt{106}$
∵100<106<121,
∴10$<\sqrt{106}$<11,
∴x在10和11之间;
(2)∵10.22=104.04,10.32=106.09,
∴10.2<$\sqrt{106}$<10.3,
∴把x的结果精确到十分位,x的值在10.2和10.3两个数之间;
∵10.292=105.8841,10.302=106.09,
∴10.29<$\sqrt{106}$<10.30,
∴把x的结果精确到百分位,x的值在10.29和10.30两个数之间.
点评 本题主要考查了估算无理数的大小,利用“夹逼法”是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
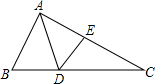 如图,在△ABC中,已知AD是∠BAC的角平分线,∠B=65°,∠C=54°
如图,在△ABC中,已知AD是∠BAC的角平分线,∠B=65°,∠C=54°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市九校七年级3月联考数学试卷(解析版) 题型:单选题
下列三个命题:①同位角相等,两直线平行;②两点之间,线段最短;③过两点有且只有一条直线,其中真命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com