
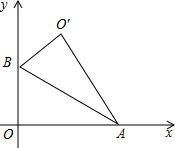
 如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为($\sqrt{3}$,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$)..
如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为($\sqrt{3}$,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).. 分析 作O′C⊥y轴于点C,首先根据点A,B的坐标分别为($\sqrt{3}$,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=$\sqrt{3}$x,利用勾股定理求得x的值即可求解.
解答  解:如图,作O′C⊥y轴于点C,
解:如图,作O′C⊥y轴于点C,
∵点A,B的坐标分别为($\sqrt{3}$,0),(0,1),
∴OB=1,OA=$\sqrt{3}$,
∴tan∠BAO=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BAO=30°,
∴∠OBA=60°,
∵Rt△AOB沿着AB对折得到Rt△AO′B,
∴∠CBO′=60°,
∴设BC=x,则OC′=$\sqrt{3}$x,
∴x2+($\sqrt{3}$x)2=1,
解得:x=$\frac{1}{2}$(负值舍去),
∴O′C=$\frac{\sqrt{3}}{2}$,
∴OC=OB+BC=1+$\frac{1}{2}$=$\frac{3}{2}$,
∴点O′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
故答案为:($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
点评 本题考查了翻折变换及坐标与图形的性质的知识,解题的关键是根据点A和点B的坐标确定三角形为特殊三角形,难度不大.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
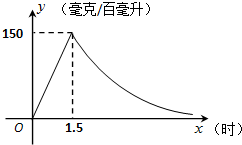 实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com