
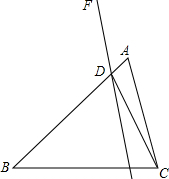
 如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.
如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.分析 (1)根据DF∥AC,得到∠CDE=∠ACD,由∠BDC=∠ACB,得到∠BDE=∠BCD,根据对顶角相等得到∠FDA=∠BDE,所以∠FDA=∠BCD.
(2)分两种情况,分别画出图形,利用三角形的内角和与外角的性质即可解答.
解答 解:(1)如图1,
∵DF∥AC,
∴∠CDE=∠ACD,
∵∠BDC=∠ACB,
∴∠BDE+∠CDE=∠ACD+BCD,
∴∠BDE=∠BCD,
∵∠FDA=∠BDE,
∴∠FDA=∠BCD.
(2)当DF交AC于点H时,如图2,
在△BDC中,∠B+∠BDC+∠BCD=180°,
在△ABC中,∠B+∠ACB+∠A=180°,
∵∠BDC=∠ACB,
∴∠A=∠BCD,
∵在△ADH中,∠A+∠ADH+∠AHD=180°,
∴∠BCD+∠ADH+∠AHD=180°.
当DF交射线CA与点H时,如图3,
∵∠BAC=∠ADH+∠AHD(外角的性质),∠BAC=∠BCD,
∴∠BCD=∠ADH+∠AHD.
点评 本题考查了平行线的性质,三角形的内角和,外角的性质,在(2)中,分两种情况画出图形是解决本题的关键.


科目:初中数学 来源: 题型:选择题
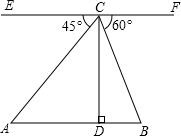 如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.
如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.| A. | 30+10$\sqrt{3}$ | B. | 40$\sqrt{3}$ | C. | 45 | D. | 30+15$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )| A. | 2≤k≤4 | B. | 2≤k≤5 | C. | 2≤k≤8 | D. | 5≤k≤8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )| A. | 300($\sqrt{3}$+1)m | B. | 1200($\sqrt{3}$-1)m | C. | 1800($\sqrt{3}$-1)m | D. | 2400($\sqrt{2}$-1)m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
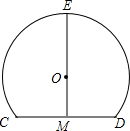 一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com