



科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
某学校为了改善教职工居住条件,准备在教学楼(正楼)的正南方向建一座住宅楼(正楼),要求住宅楼与教学楼等高,均为15.6米,已知该地区冬至正午时分太阳高度最低,太阳光线与水平线的夹角为30°.如果住宅楼与教学楼间相距19.2米,如下图所示,
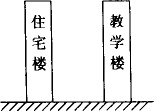
(1)此时住宅楼的影子落在教学楼上有多高?(精确到0.1米)
(2)要使住宅楼的影子刚好落在教学楼的墙角,则两楼间的距离应是多少?(精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010-2011学年湖北省黄石市阳新三中九年级(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com