
”¾ĢāÄæ”æÄ³Ń§Š£×éÖÆĘßÄź¼¶Ń§Éś½ųŠŠ”°Ą¬»ų·ÖĄą”±ÖŖŹ¶²āŹŌ£¬ĻÖĖ껜³éČ”²æ·ÖѧɜµÄ³É¼Ø½ųŠŠĶ³¼Ę£¬²¢»ęÖĘČēĻĀʵŹż·Ö²¼±ķŅŌ¼°ĘµŹż·Ö²¼Ö±·½Ķ¼£®
·ÖŹżµµ | ·ÖŹż¶Ī/·Ö | ʵŹż | ʵĀŹ |
A | 90£¼x”Ü100 | a | 0.12 |
B | 80£¼x”Ü90 | b | 0.18 |
C | 70£¼x”Ü80 | 20 | c |
D | 60£¼x”Ü70 | 15 | d |
Ēėøł¾ŻŅŌÉĻŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
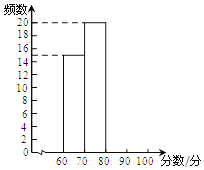
£Ø1£©ŅŃÖŖA£¬BµµµÄѧɜČĖŹżÖ®ŗĶµČÓŚDµµŃ§ÉśČĖŹż£¬Ēó±»³éČ”µÄѧɜČĖŹż£¬²¢°ŃʵŹż·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£®
£Ø2£©øĆŠ£ĘßÄź¼¶¹²ÓŠ200Ćūѧɜ²Ī¼Ó²āŹŌ£¬Ēė¹Ą¼ĘĘßÄź¼¶³É¼ØŌŚCµµµÄѧɜČĖŹż£®
£Ø3£©ÄćÄÜČ·¶Ø±»³éČ”µÄÕāŠ©Ń§ÉśµÄ³É¼ØµÄÖŚŹżŌŚÄÄŅ»µµĀš£æĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©±»³éČ”µÄѧɜӊ 50£ØĆū£©£»¼ū½āĪö£»£Ø2£©ĘßÄź¼¶³É¼ØŌŚCµµµÄѧɜӊ80ČĖ£»£Ø3£©ÖŚŹżŌŚCµµ£¬ĄķÓɼū½āĪö
”¾½āĪö”æ
£Ø1£©øł¾ŻA£¬BµµµÄѧɜČĖŹżÖ®ŗĶµČÓŚDµµŃ§ÉśČĖŹżŗĶA£¬BµµµÄʵĀŹæÉŅŌĒóµĆ±¾“Īµ÷²éµÄѧɜČĖŹż£¬Č»ŗóŌŁĒó³öAµµŗĶBµµµÄČĖŹż¼“æɽ«ĘµŹż·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£»
£Ø2£©øł¾ŻĘµŹż·Ö²¼±ķÖŠµÄŹż¾ŻæÉŅŌĒóµĆĘßÄź¼¶³É¼ØŌŚCµµµÄѧɜČĖŹż£»
£Ø3£©øł¾ŻĢāŅāŗĶʵŹż·Ö²¼±ķÖŠµÄŹż¾ŻæÉŅŌĒóµĆÖŚŹżŌŚÄÄŅ»µµ£¬±¾ĢāµĆŅŌ½ā¾ö£®
(1)øł¾ŻA£¬BµµµÄѧɜČĖŹżÖ®ŗĶµČÓŚDµµŃ§ÉśČĖŹżÖŖ£ŗA£¬BµµµÄѧɜČĖŹżÖ®ŗĶĪŖ15(Ćū)£¬
”ą±»³éČ”µÄѧɜӊ£ŗ15”Ā(0.12+0.18)=50(Ćū)£¬
BµµČĖŹżĪŖ£ŗ50”Į0.18=9£¬
AµµČĖŹżĪŖ£ŗ50”Į0.12=6£¬
²¹Č«µÄʵŹż·Ö²¼Ö±·½Ķ¼ČēĶ¼ĖłŹ¾£»

(2)200”Į![]() =80(ČĖ)£¬
=80(ČĖ)£¬
¼“ĘßÄź¼¶³É¼ØŌŚCµµµÄѧɜӊ80ČĖ£»
(3)±»³éČ”µÄÕāŠ©Ń§ÉśµÄ³É¼ØµÄÖŚŹżŌŚCµµ£¬
ĄķÓÉ£ŗ”ßAµµÓŠ6ČĖ£¬BµµÓŠ9ČĖ£¬CµµÓŠ20ČĖ£¬DµµÓŠ15ČĖ£¬
”ąÖŚŹżŌŚCµµ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠµÄµć
ÖŠµÄµć![]() £¬½«ĖüµÄׯ×ų±ź
£¬½«ĖüµÄׯ×ų±ź![]() Óėŗį×ų±ź
Óėŗį×ų±ź![]() µÄ±Č
µÄ±Č![]() ³ĘĪŖµć
³ĘĪŖµć![]() µÄ”°ĄķĻėÖµ”±£¬¼Ē×÷
µÄ”°ĄķĻėÖµ”±£¬¼Ē×÷![]() £®Čē
£®Čē![]() µÄ”°ĄķĻėÖµ”±
µÄ”°ĄķĻėÖµ”±![]() £®
£®
£Ø1£©¢ŁČōµć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻ£¬Ōņµć
ÉĻ£¬Ōņµć![]() µÄ”°ĄķĻėÖµ”±
µÄ”°ĄķĻėÖµ”±![]() µČÓŚ_______£»
µČÓŚ_______£»
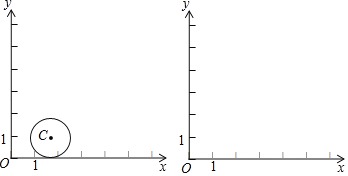
¢ŚČēĶ¼£¬![]() £¬
£¬![]() µÄ°ė¾¶ĪŖ1£®Čōµć
µÄ°ė¾¶ĪŖ1£®Čōµć![]() ŌŚ
ŌŚ![]() ÉĻ£¬Ōņµć
ÉĻ£¬Ōņµć![]() µÄ”°ĄķĻėÖµ”±
µÄ”°ĄķĻėÖµ”±![]() µÄȔֵ·¶Ī§ŹĒ_______£®
µÄȔֵ·¶Ī§ŹĒ_______£®
£Ø2£©µć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻ£¬
ÉĻ£¬![]() µÄ°ė¾¶ĪŖ1£¬µć
µÄ°ė¾¶ĪŖ1£¬µć![]() ŌŚ
ŌŚ![]() ÉĻŌĖ¶ÆŹ±¶¼ÓŠ
ÉĻŌĖ¶ÆŹ±¶¼ÓŠ![]() £¬Ēóµć
£¬Ēóµć![]() µÄŗį×ų±ź
µÄŗį×ų±ź![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø3£©![]() £¬
£¬![]() ŹĒŅŌ
ŹĒŅŌ![]() ĪŖ°ė¾¶µÄ
ĪŖ°ė¾¶µÄ![]() ÉĻČĪŅāŅ»µć£¬µ±
ÉĻČĪŅāŅ»µć£¬µ±![]() Ź±£¬»³öĀś×ćĢõ¼žµÄ×ī“óŌ²£¬²¢Ö±½ÓŠ“³öĻąÓ¦µÄ°ė¾¶
Ź±£¬»³öĀś×ćĢõ¼žµÄ×ī“óŌ²£¬²¢Ö±½ÓŠ“³öĻąÓ¦µÄ°ė¾¶![]() µÄÖµ£®£ØŅŖĒó»Ķ¼Ī»ÖĆ×¼Č·£¬µ«²»±Ų³ß¹ę×÷Ķ¼£©
µÄÖµ£®£ØŅŖĒó»Ķ¼Ī»ÖĆ×¼Č·£¬µ«²»±Ų³ß¹ę×÷Ķ¼£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬OĪŖ×ų±źŌµć£¬”÷AOBŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻAOB=90”ć£¬µćA£Ø2,1£©.
£Ø1£©ĒóµćBµÄ×ų±ź£»
£Ø2£©Ēó¾¹żA”¢O”¢BČżµćµÄÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø3£©ŌŚ£Ø2£©ĖłĒóµÄÅ×ĪļĻßÉĻ£¬ŹĒ·ń“ęŌŚŅ»µćP£¬Ź¹ĖıߊĪABOPµÄĆ껿×ī“ó£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
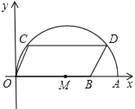
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćAµÄ×ų±źŹĒ£Ø10£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø8£¬0£©£¬µćC£¬DŌŚŅŌOAĪŖÖ±¾¶µÄ°ėŌ²MÉĻ£¬ĒŅĖıߊĪOCDBŹĒĘ½ŠŠĖıߊĪ£¬ŌņµćCµÄ×ų±źĪŖ______.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
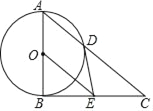
”¾ĢāÄæ”æČēĶ¼£¬ŅŌRt”÷ABCµÄÖ±½Ē±ßABĪŖÖ±¾¶×÷”ŃO½»Š±±ßACÓŚµćD£¬¹żŌ²ŠÄO×÷OE”ĪAC£¬½»BCÓŚµćE£¬Į¬½ÓDE£®
£Ø1£©ÅŠ¶ĻDEÓė”ŃOµÄĪ»ÖĆ¹ŲĻµ²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ĒóÖ¤£ŗ2DE2=CDOE£»
£Ø3£©ČōtanC=![]() £¬DE=
£¬DE=![]() £¬ĒóADµÄ³¤£®
£¬ĒóADµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Rt”÷OABµÄ¶„µćAŌŚxÖįµÄÕż°ėÖįÉĻ£¬¶„µćBµÄ×ų±źĪŖ(3£¬![]() )£¬µćCµÄ×ų±źĪŖ(1£¬0)£¬µćPĪŖŠ±±ßOBÉĻµÄŅ»¶Æµć£¬ŌņPA+PCµÄ×īŠ”Öµ_____£®
)£¬µćCµÄ×ų±źĪŖ(1£¬0)£¬µćPĪŖŠ±±ßOBÉĻµÄŅ»¶Æµć£¬ŌņPA+PCµÄ×īŠ”Öµ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¾ŲŠĪOABCµÄ¶„µćBµÄ×ų±źĪŖ£Ø4£¬2£©£¬Ö±Ļßy=©![]() x+
x+![]() Óė±ßAB£¬BC·Ö±šĻą½»ÓŚµćM£¬N£¬ŗÆŹży=
Óė±ßAB£¬BC·Ö±šĻą½»ÓŚµćM£¬N£¬ŗÆŹży=![]() £Øx£¾0£©µÄĶ¼Ļó¹żµćM£®
£Øx£¾0£©µÄĶ¼Ļó¹żµćM£®
£Ø1£©ŹŌĖµĆ÷µćNŅ²ŌŚŗÆŹży=![]() £Øx£¾0£©µÄĶ¼ĻóÉĻ£»
£Øx£¾0£©µÄĶ¼ĻóÉĻ£»
£Ø2£©½«Ö±ĻßMNŃŲyÖįµÄøŗ·½ĻņĘ½ŅʵƵ½Ö±ĻßM”äN”䣬µ±Ö±ĻßM”äN”äÓėŗÆŹżyØT![]() £Øx£¾0£©µÄĶ¼Ļó½öÓŠŅ»øö½»µćŹ±£¬ĒóÖ±ĻßM'N”äµÄ½āĪöŹ½£®
£Øx£¾0£©µÄĶ¼Ļó½öÓŠŅ»øö½»µćŹ±£¬ĒóÖ±ĻßM'N”äµÄ½āĪöŹ½£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ![]() µÄČżøö¶„µć×ų±ź·Ö±šŹĒ
µÄČżøö¶„µć×ų±ź·Ö±šŹĒ![]() £¬
£¬![]() £¬
£¬![]() £®
£®
£Ø1£©Ēė×÷³ö![]() ČĘ
ČĘ![]() µćÄꏱÕėŠż×Ŗ
µćÄꏱÕėŠż×Ŗ![]() µÄ
µÄ![]() £»
£»
£Ø2£©ŅŌµć![]() ĪŖĪ»ĖĘÖŠŠÄ£¬½«
ĪŖĪ»ĖĘÖŠŠÄ£¬½«![]() Ą©“óĪŖŌĄ“µÄ2±¶£¬µĆµ½
Ą©“óĪŖŌĄ“µÄ2±¶£¬µĆµ½![]() £¬ĒėŌŚ
£¬ĒėŌŚ![]() ÖįµÄ×ó²ą»³ö
ÖįµÄ×ó²ą»³ö![]() £»
£»
£Ø3£©ĒėÖ±½ÓŠ“³ö![]() µÄÕżĻŅÖµ£®
µÄÕżĻŅÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪ![]() ŗĶÕżČż½ĒŠĪ
ŗĶÕżČż½ĒŠĪ![]() ¶¼ÄŚ½ÓÓŚ
¶¼ÄŚ½ÓÓŚ![]() £¬
£¬![]() Óė
Óė![]() £¬
£¬![]() ·Ö±šĻą½»ÓŚµć
·Ö±šĻą½»ÓŚµć![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() µÄÖµŹĒ________£®
µÄÖµŹĒ________£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com