
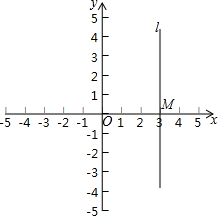 如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.分析 (1)根据关于y轴对称点的坐标特点是横坐标互为相反数,纵坐标相同可以得到△A1B1C1各点坐标,又关于直线l的对称图形点的坐标特点是纵坐标相同,横坐标之和等于3的二倍,由此求出△A2B2C1的三个顶点的坐标;
(2)P与P1关于y轴对称,利用关于y轴对称点的特点:纵坐标不变,横坐标变为相反数,求出P1的坐标,再由直线l的方程为直线x=3,利用对称的性质求出P2的坐标,即可得出PP2的长.
解答 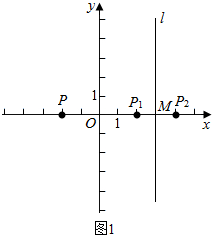 解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);
解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);
(2)如图1,当0<a<3时,∵P与P1关于y轴对称,P(-a,0),
∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得:$\frac{x+a}{2}$=3,即x=6-a,
∴P2(6-a,0),
则PP2=6-a-(-a)=6-a+a=6.
点评 本题考查学生“轴对称”与坐标的相关知识的试题,掌握轴对称的性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
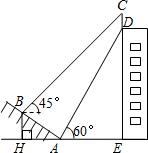 如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.
如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com