

分析 (1)①根据直径的性质,由DE∥AB得$\frac{CD}{CB}$=$\frac{CE}{CA}$即可解决问题.②求出BD、AE即可解决问题;
(2)只要证明△ACE∽△BCD即可;
(3)求出AB、AE,利用△ACE∽△BCD即可解决问题;
(4)分类讨论:①如图5中,当α=90°时,半圆与AC相切,②如图6中,当α=90°+∠ACB时,半圆与BC相切,分别求出BD即可.
解答 (1)解:①如图1中 
当α=0时,连接DE,则∠CDE=90°,
∵∠CDE=∠B=90°,
∴DE∥AB,
∴$\frac{CD}{CB}$=$\frac{CE}{AC}$=$\frac{1}{2}$,
∵BC=m,
∴CD=$\frac{1}{2}$m,
故答案为90°,$\frac{1}{2}$m,
②如图2中,当α=180°时,BD=BC+CD=$\frac{3}{2}$m,AE=AC+CE=$\frac{3}{2}$n,
∴$\frac{BD}{AE}$=$\frac{m}{n}$.
故答案为$\frac{m}{n}$;
(2)如图3中,
∵∠ACB=∠DCE,
∴∠ACE=∠BCD,
∵$\frac{CD}{CE}$=$\frac{BC}{AC}$=$\frac{m}{n}$,
∴△ACE∽△BCD,
∴$\frac{BD}{AE}$=$\frac{BC}{AC}$=$\frac{m}{n}$;
(3)如图4中,当α=∠ACB时,
在Rt△ABC中,∵AC=5,BC=4,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=3,
在Rt△ABE中.∵AB=3,BE=BC-CE=1.5,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3}{2}$$\sqrt{5}$,
由(2)可知△ACE∽△BCD,
∴$\frac{BD}{AE}$=$\frac{BC}{AC}$,
∴$\frac{BD}{\frac{3}{2}\sqrt{5}}$=$\frac{4}{5}$,
∴BD=$\frac{6\sqrt{5}}{5}$,
故答案为$\frac{6\sqrt{5}}{5}$;
(4)∵m=4$\sqrt{2}$,n=6,
∴CE=3,CD=2$\sqrt{2}$,AB=$\sqrt{C{A}^{2}-B{C}^{2}}$=2,
①如图5中,当α=90°时,半圆与AC相切,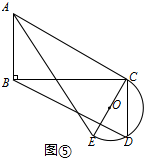
在Rt△DBC中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=2$\sqrt{10}$.
②如图6中,当α=90°+∠ACB时,半圆与BC相切,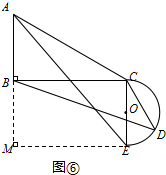
作EM⊥AB于M,
∵∠M=∠CBM=∠BCE=90°,
∴四边形BCEM是矩形,
∴BM=CE=3,ME=4$\sqrt{2}$,
∴AM=5,AE=$\sqrt{A{M}^{2}+M{E}^{2}}$=$\sqrt{57}$,
由(2)可知$\frac{DB}{AE}$=$\frac{2\sqrt{2}}{3}$,
∴BD=$\frac{2\sqrt{114}}{3}$.
故答案为2$\sqrt{10}$或$\frac{2\sqrt{114}}{3}$.
点评 本题考查圆的有关知识,相似三角形的判定和性质、勾股定理等知识,正确画出图形是解决问题的关键,学会分类讨论的思想,本题综合性比较强,属于中考压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明在大楼45米高(即PH=45米)的窗户P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$.点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732.
如图,小明在大楼45米高(即PH=45米)的窗户P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$.点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
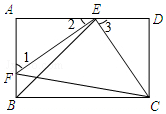 如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com