
 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可)
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可) 分析 首先根据平行线的性质可得∠1=∠DEF,再根据∠1=∠2,可得∠2=∠DEF,再根据等角对等边可得DF=FE;根据平行四边形的性质可得DF∥AE,再由EF∥AD,可得四边形ADFE是平行四边形,再根据平行四边形的性质可得DF=AE;首先证明∠2+∠3=90°,根据勾股定理可得CG2+DG2=CD2.
解答 解:①∵EF∥AD,
∴∠1=∠DEF,
∵∠1=∠2,
∴∠2=∠DEF,
∴DF=FE,
∵四边形ABCD是平行四边形,
∴DF∥AE,
∵EF∥AD,
∴四边形ADFE是平行四边形,
∴DF=AE;
②∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠ADC+∠DCB=180°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=90°,
∴∠DGC=90°,
∴CG2+DG2=CD2;
故答案为:DF=FE,DF=AE;CG2+DG2=CD2.
点评 此题主要考查了平行四边形的性质,以及勾股定理,关键是掌握平行四边形对边平行且相等.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
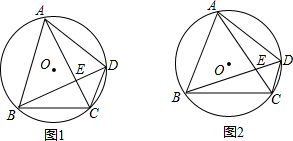
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
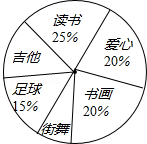 九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题:
九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
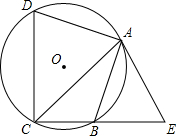 如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°
如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com