
| 3 |
| 2 |
| A.3s | B.4s | C.5s | D.6s |
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源:不详 题型:解答题
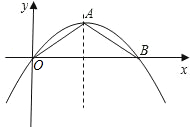
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
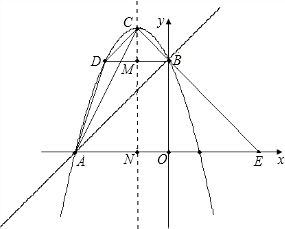 经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.
经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
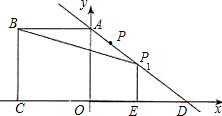 形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
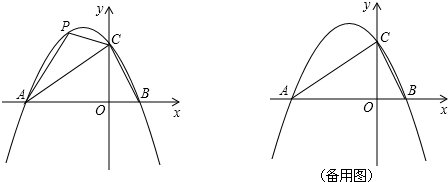
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
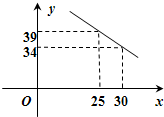 4万元,且所有资金全部用于生产这三种型号的汽车,三种型号的汽车生产成本和售价如下表:
4万元,且所有资金全部用于生产这三种型号的汽车,三种型号的汽车生产成本和售价如下表:| A | B | C | |
| 成本(万元/辆) | 12 | 15 | 18 |
| 售价(万元/辆) | 14 | 18 | 22 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com