
平面直角坐标第xoy中,A点的坐标为(0,5).B、C分别是x轴、y轴上的两个动点,C从A出发,沿y轴负半轴方向以1个单位/秒的速度向点O运动,点B从O出发,沿x轴正半轴方向以1个单位/秒的速度运动.设运动时间为t秒,点D是线段OB上一点,且BD=OC.点E是第一象限内一点,且AE DB.
DB.
(1)当t=4秒时,求过E、D、B三点的抛物线解析式.
(2)当0<t<5时,(如图甲),∠ECB的大小是否随着C、B的变化而变化?如果不变,求出它的大小.
(3)求证:∠APC=45°
(4)当t>5时,(如图乙)∠APC的大小还是45°吗?请说明理由.

(1)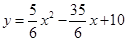 ;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.
;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.
解析试题分析:(1)当t=4时,知AC=OB=4,进而知OC=1,由BD=OC,AE∥DB,AE=BD可求AE=DB=OC=1,点E、点D、点B的坐标即可确定。再设出抛物线的解析式y=ax2+bx+c,将三点坐标代入即可求出a、b、c的值;
(2)连接CE,可证∠ECB=90°;
(3)由(2)可知:△ECB是等腰直角三角形,继而可证四边形ADBE是平行四边形,从而∠APC=∠EBC=45°;
(4)如图,在第二象限取点F,作AF∥BD,AF=BD,连接CF、BF.易得Rt△ACF≌Rt△OBC,再证△BCF是等腰直角三角形,由三角形的一个外角大于与它不相邻的内角知∠APC>45°.
(1)当t=4秒时,AC=OB=4,由A(0,5)得C(0,1),即OC=1.
又BD=OC,AE DB,
∴AE=DB=OC=1.
∴E(1,5)B(4,0),D(3,0).
设过E、D、B三点的抛物线解析式为y="ax2+bx+c" ,则有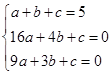 ,解得:
,解得: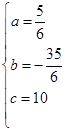 ;
;
∴抛物线解析式为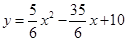 ;
;
(2)(2)∠ECB的大小不变。
连接CE。易得Rt△ACE≌Rt△OBC(SAS)
∴CE=CB,∠ACE=∠OBC,∠AEC=∠OCB.
又∠ACE+∠AEC=90°,
∴∠ACE+∠OCB=90°
,∴∠ECB=90°.
(3)由(2)知,CE=CB,∠ECB=90°,
∴△ECB是等腰直角三角形.
∴∠EBC=45°,
又AE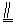 DB,
DB,
∴四边形ADBE是平行四边形.
∴AB∥EB.
∴∠APC=∠EBC=45°.
(4)当t>5时,∠APC>45°,理由如下:
如图,在第二象限取点F,作AF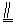 BD,连接CF、BF.
BD,连接CF、BF.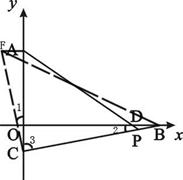
易得Rt△ACF≌Rt△OBC(SAS)
∴CF=CB,∠1=∠2.
又∠1+∠3=90°。∴∠2+∠3=90°即△BCF是等腰直角三角形.
∴∠CBF=45°,又∠APC>∠CBF,
∴∠APC>45°.
考点:1.二次函数关系式;2.三角形全等的判定与性质.


科目:初中数学 来源: 题型:解答题
如图,矩形OABC在平面直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O、A两点,直线AC交抛物线于点D。
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以点A、D、M、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:二次函数
 中的
中的 满足下表:
满足下表:
 | …… |  | 0 | 1 | 2 | 3 | …… |
 | …… | 0 |  |  |  |  | …… |
 的值;
的值; 时的
时的 的取值范围;
的取值范围; ,
, 两点都在该函数图象上,且
两点都在该函数图象上,且 ,试比较
,试比较 与
与 的大小.
的大小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角坐标系xOy中,正方形OCBA的顶点A,C分别在y轴,x轴上,点B坐标为(6,6),抛物线y=ax2+bx+c经过点A,B两点,且3a-b=-1.
(1)求a,b,c的值;
(2)如果动点E,F同时分别从点A,点B出发,分别沿A→B,B→C运动,速度都是每秒1个单位长度,当点E到达终点B时,点E,F随之停止运动,设运动时间为t秒,△EBF的面积为S.
①试求出S与t之间的函数关系式,并求出S的最大值;
②当S取得最大值时,在抛物线上是否存在点R,使得以E,B,R,F为顶点的四边形是平行四边形?如果存在,求出点R的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
函数y =ax²(a≠0)与直线y =2x-3的图像交于点(1,b).
求:(1)a和b的值;
(2)求抛物线y =ax²的开口方向、对称轴、顶点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,),其顶点在直线y=-2x上.
(1)求a,b的值;
(2)写出当-2≤x≤2时,二次函数y的取值范围;
(3)以AC、CB为一组邻边作□ACBD,则点D关于x轴的对称点D’是否在该二次函数的图象上?请说明理由.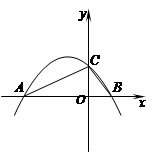
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
学习了函数的知识后,数学活动小组到文具店调研一种进价为每支2元的活动笔的销售情况。调查后发现,每支定价3元,每天能卖出100支,而且每支定价每下降0.1元,其销售量将增加10支。但是物价局规定,该活动笔每支的销售利润不能超过其进价的40%。设每支定价x元,每天的销售利润为y元。
(1)求每天的销售利润为y与每支定价x之间的函数关系式;
(2)如果要实现每天75元的销售利润,那么每支定价应为多少元?
(3)当每支定价为多少元时,可以使这种笔每天的销售利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为:y1= 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=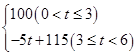
(1)用x的代数式表示t,则t=__________;当0<x≤3时,y2与x的函数关系式为:y2=__________________;当3≤x<________时,y2=100;
(2)当3≤x<6时,求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数关系式,并求此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com