
分析 根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.
解答 解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,AD=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴sin∠AOE=$\frac{AE}{AO}$=$\frac{\sqrt{2}}{2}$,sin∠AOD=$\frac{AD}{AO}$=$\frac{1}{2}$,
∴∠AOE=45°,∠AOD=30°,
∴∠BAO=60°,∠CAO=90°-45°=45°,
∴∠BAC=45°+60°=105°,或∠BAC′=60°-45°=15°.
∴∠BAC=15°或105°.
故答案是:15°或105°.
点评 本题考查的是垂径定理及直角三角形的性质,解答此题时进行分类讨论,不要漏解.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
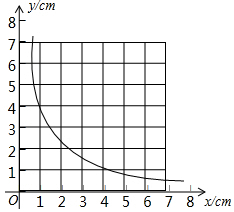 一个三角形的面积始终保持不变,它的一边的长为xcm,这边上的高为ycm,y与x的关系如图,根据图中给出的信息,解答下列问题:
一个三角形的面积始终保持不变,它的一边的长为xcm,这边上的高为ycm,y与x的关系如图,根据图中给出的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-6=(10-x)2 | B. | x2-62=(10-x)2 | C. | x2+6=(10-x)2 | D. | x2+62=(10-x)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
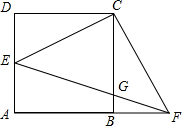 如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解长江中鱼的种类 | B. | 对“最强大脑”节目收视率的调查 | ||
| C. | 调查我国网名对某事件的看法 | D. | 对某班50名同学体重情况的调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com