
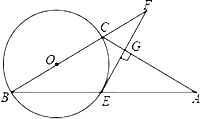
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
【答案】(1)证明见解析;(2)CG=![]() .
.
【解析】分析: (1)证明OE是△ABC的中位线,得出OE∥AC,再由已知条件得出FE⊥OE,即可得出结论;
(2)由切割线定理求出直径,得出半径的长,由平行线得出三角形相似,得出比例式,即可得出结果.
详解:
(1)证明:连接CE,
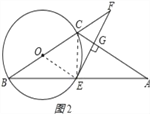
∵BC是直径,
∴∠BEC=90°,
∴CE⊥AB;
又∵AC=BC,
∴AE=BE.
连接OE,
∵BE=AE,OB=OC,
∴OE是△ABC的中位线,
∴OE∥AC,AC=2OE=6.
又∵EG⊥AC,
∴FE⊥OE,
∴FE是⊙O的切线.
(2)∵EF是⊙O的切线,∠CEF+∠CEO=900,且BC是直径
∴∠BEO+∠CEO=900
∴∠CEF=∠BEO,∠F为公共角,
∴ΔCEF∽ΔEBF
∴FE2=FCFB.
设FC=x,则有2FB=16,
∴FB=8,
∴BC=FB﹣FC=8﹣2=6,
∴OB=OC=3,即⊙O的半径为3;
∴OE=3,
∵OE∥AC,
∴△FCG∽△FOE,
∴![]() ,即
,即![]() ,
,
解得:CG=![]() .
.
点睛: 本题考查了切线的判定、等腰三角形的性质、三角形中位线的判定、切割线定理、相似三角形的判定与性质;熟练掌握切线的判定,由三角形中位线定理得出OE∥AC是解决问题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下述材料,尝试解决问题
数学是一门充满思维乐趣的学科,现有一个![]() 的数阵
的数阵![]() ,数阵
,数阵![]() 中每个位置对应的数都是1,2或3. 定义
中每个位置对应的数都是1,2或3. 定义![]() 为数阵中第
为数阵中第![]() 行、第
行、第![]() 列的数. 例如,数阵
列的数. 例如,数阵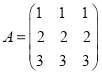 第3行、第2列所对应的数是3,所以
第3行、第2列所对应的数是3,所以![]() .
.
(1)对于数阵![]() ,
,![]() 的值为_________;若
的值为_________;若![]() ,则
,则![]() 的值为_________.
的值为_________.
(2)若一个![]() 的数阵对任意的
的数阵对任意的![]() 均满足以下条件:
均满足以下条件:
条件一:![]() ;
;
条件二:![]() ;则称这个数阵是“有趣的”.
;则称这个数阵是“有趣的”.
已知一个“有趣的”数阵满足![]() ,试计算
,试计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司改革实行每月考核再奖励的新制度,大大调动了员工的积极性,![]() 年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
钱数变化 |
|
|
|
|
|
|
|
(1)若![]() 年底
年底![]() 月份奖金为
月份奖金为![]() 元,用代数式表示
元,用代数式表示![]() 年二月的奖金;
年二月的奖金;
(2)请判断七个月以来这名员工得到奖金最多是哪个月?最少是哪个月?他们相差多少元?
(3)若![]() 年这七个月中这名员工最多得到的奖金是
年这七个月中这名员工最多得到的奖金是![]() 元,请问
元,请问![]() 年
年![]() 月份他得到多少奖金?
月份他得到多少奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=8,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
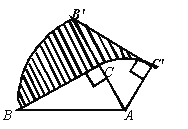
A. 8π B. 6π C. 4π D. 2π
查看答案和解析>>
科目:初中数学 来源: 题型:
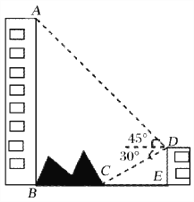
【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上). 已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果精确到0.1m)
(参考数据: ![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
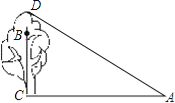
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面内有不共线的3个点,![]() ,
,![]() ,
,![]() .
.
(1)作射线![]() ,在
,在![]() 延长线上取一点
延长线上取一点![]() ,使
,使![]() ;
;
(2)作线段![]() 并延长
并延长![]() 到点
到点![]() ,使
,使![]() ;
;
(3)连接![]() ,
,![]() ;
;
(4)度量线段![]() 和
和![]() 的长度,直接写出二者之间的数量关系,观察
的长度,直接写出二者之间的数量关系,观察![]() 和
和![]() 的位置是(填“平行”或“相交”)关系;
的位置是(填“平行”或“相交”)关系;
(5)作![]() 的中点
的中点![]() ,连接
,连接![]() ,猜想
,猜想![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com