
 ,∠A=45°,以AB所在直线为x轴,A为坐标原点建立直角坐标系,将等腰梯形ABCD饶A点按逆时针方向旋转90°得到等腰梯形OEFG(O﹑E﹑F﹑G分别是A﹑B﹑C﹑D旋转后的对应点)(图1)
,∠A=45°,以AB所在直线为x轴,A为坐标原点建立直角坐标系,将等腰梯形ABCD饶A点按逆时针方向旋转90°得到等腰梯形OEFG(O﹑E﹑F﹑G分别是A﹑B﹑C﹑D旋转后的对应点)(图1)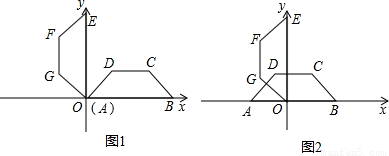
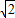 ,∠A=∠C=45°,用正弦或余弦函数就能求出),那么C点的坐标就应该是(4,2).而F点的横坐标的绝对值等于C点纵坐标的绝对值,F点的纵坐标的绝对值等于C点横坐标的绝对值,因此F的坐标应是(-2,4).
,∠A=∠C=45°,用正弦或余弦函数就能求出),那么C点的坐标就应该是(4,2).而F点的横坐标的绝对值等于C点纵坐标的绝对值,F点的纵坐标的绝对值等于C点横坐标的绝对值,因此F的坐标应是(-2,4). x,那么三角形AQO的面积=
x,那么三角形AQO的面积= ×(
×( x)2=
x)2= x2.在上面我们求出了DH的长,那么梯形AOHD的面积=
x2.在上面我们求出了DH的长,那么梯形AOHD的面积= ×(x-2+x)×2=2x-2.因此重合部分的面积=梯形ADHO的面积-三角形AQM的面积=-
×(x-2+x)×2=2x-2.因此重合部分的面积=梯形ADHO的面积-三角形AQM的面积=- x2+2x-2.也就求出了x、y的函数关系式.
x2+2x-2.也就求出了x、y的函数关系式.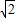 ,∠DOM=45°,
,∠DOM=45°, ×(DH+OA)×DM=2x-2.
×(DH+OA)×DM=2x-2.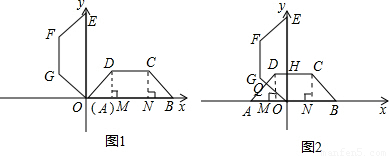
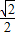 x,
x, ×AQ×OQ=
×AQ×OQ= x2
x2 x2
x2 x2+2x-2(2<x<4)
x2+2x-2(2<x<4)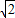 ,
, )2=m2+(2-6)2,
)2=m2+(2-6)2, ,
, )2=(m+2)2+(2-4)2,即m(m+4)=0,m=-4,m=0.
)2=(m+2)2+(2-4)2,即m(m+4)=0,m=-4,m=0.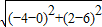 =4
=4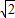 =2EF,
=2EF,

科目:初中数学 来源: 题型:
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且查看答案和解析>>
科目:初中数学 来源: 题型:
 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com