
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��0��a����B��b��a������a��b���㣨a��3��2+|b��6|��0����ͬʱ����A��B�ֱ�����ƽ��3����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��

��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD��
��2����y�����Ƿ����һ��M������MC��MD��ʹS��MCD��![]() S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����P��ֱ��BD�ϵ�һ�����㣬����PA��PO������P��BD���ƶ�ʱ������B��D�غϣ���ֱ��д����BAP����DOP����APO֮�������������ϵ��
���𰸡���1��18����2��M��0��2����0����2������3���ٵ���P���߶�BD���ƶ�ʱ����APO����DOP+��BAP���ڵ���P��DB���ӳ�����ʱ����DOP����BAP+��APO���۵���P��BD���ӳ�����ʱ����BAP����DOP+��APO��
��������
��1�����ݷǸ��������ʷֱ����a��b������ƽ�ƹ��ɵõ���C��D�����꣬����������ͼ�ε��������S�ı���ABCD��
��2����M����Ϊ��0��m�������������ε������ʽ�г����̣��ⷽ�����m���õ���M�����ꣻ
��3���ֵ�P���߶�BD�ϡ���P��DB���ӳ����ϡ���P��BD���ӳ������������������ƽ���ߵ����ʽ��
�⣺��1���ߣ�a��3��2+|b��6|��0��
��a��3��0��b��6��0��
����ã�a��3��b��6��
��A��0��3����B��6��3����
�߽���A��B�ֱ�����ƽ��3����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D��
��C����2��0����D��4��0����
��S�ı���ABDC��AB��OA��6��3��18��
��2����y���ϴ���һ��M��ʹS��MCD��S�ı���ABCD��
��M������0��m����
��S��MCD��![]() S�ı���ABDC��
S�ı���ABDC��
��![]() ��6|m|��
��6|m|��![]() ��18��
��18��
���m����2��
��M��0��2����0����2����
��3���ٵ���P���߶�BD���ƶ�ʱ����APO����DOP+��BAP��
�������£���ͼ1������P��PE��AB��
��CD��ABƽ�Ƶõ�����CD��AB��
��PE��CD��
���BAP����APE����DOP����OPE��
���BAP+��DOP����APE+��OPE����APO��
�ڵ���P��DB���ӳ�����ʱ��ͬ�ٵķ����ã�
��DOP����BAP+��APO��
�۵���P��BD���ӳ�����ʱ��ͬ�ٵķ����ã�
��BAP����DOP+��APO��


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=�� ![]() x2
x2 ![]() x��x�ύ��O��A����B�����������Һ�����Ϊ2��
x��x�ύ��O��A����B�����������Һ�����Ϊ2��
��1����ͼ1����AOB������Ƕ��٣�
��2����ͼ1�����߶�AB�Ϸ�������������һ��K������ABK��������ʱ�����K�����꼰��ABK�������
��3���ڣ�2���������£���H ��y�����˶�����I��x�����˶������ı���BHIK�ܳ���Сʱ�����H��I�������Լ��ı���BHIK�ܳ�����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ���ڣ�����![]() ��ֱ�ߣ��������______�����㣻��
��ֱ�ߣ��������______�����㣻��![]() ��ֱ����ǡ������ֻ��
��ֱ����ǡ������ֻ��![]() ��ֱ����ƽ�У�����
��ֱ����ƽ�У�����![]() ��ֱ�������_____�����㣨�ú���
��ֱ�������_____�����㣨�ú���![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������M�����λ���־���Ϊ���һ�����ȣ�����M��ʮλ�������λ���ֽ���λ�ã��õ�һ���µ���λ�������dz������λ��ΪM�ġ������������磺168�ġ���������Ϊ��618��������M�İ�λ���֡�ʮλ���֡���λ��������ѡ�������һ���µ���λ���������õ���������λ����ͣ����dz������ΪM�ġ��Ž��������磺123�ġ��Ž�����Ϊ12+13+21+23+31+32=132��
��1����֤��M���䡰���������IJ��ܱ�15������
��2����һ����λ������N�����λ����Ϊ2��ʮλ����Ϊa����λ����Ϊb���Ҹ�λ���ֻ�����ȣ�a��0��b��0������N�ġ��Ž�������N֮��Ϊ24����N��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ƷA�����ۼ�Ϊÿ��900Ԫ��Ϊ����Ӧ�г��������̵갴���ۼ۵ľ����Żݺ�������40Ԫ���ۣ��Կɻ���10%�� ��������ƷA�Ľ���Ϊ����Ԫ��
��������һ����ƷB����Ϊ600Ԫ��ÿ����ƷBҲ�ɻ���10%������ƷA��B������100����Ҫʹ��100����Ʒ������6670Ԫ���������ƷA��B�ֱ�������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ����һ�����εĿյ�ABCD��Ϊ��������������Ҫ�����̻����ƻ����м佨��һ�����ΪS�ľ����̵�EFGH�����У���E��F��G��H�ֱ������ε��������ϣ�AB=a�ף�BE=BF=DG=DH=x�ף���A=60�� 
��1����S����x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��2����a=100����S�����ֵ���������ʱx��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����BDC����2����3��180�㣮
(1) �����ж�DA��CE��λ�ù�ϵ����˵�����ɣ�
(2) ��DAƽ�֡�BDC��CE��AE�ڵ�E����1��70�㣬�����FAB�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ٹ�·��ͬһ����A��B��������ͼ�����ǵ����ٹ�·����ֱ��MN�ľ���ֱ�ΪAA�䣽2 km��BB�䣽4 km��A��B�䣽8 km.Ҫ�ڸ��ٹ�·��A�䡢B��֮�佨һ������P��ʹA��B������P�ľ���֮����С���������̾��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
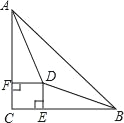
����Ŀ����ͼ��ʾ����Rt��ABC�У���C��90�㣬��BAC����ABC��ƽ�����ཻ�ڵ�D����DE��BC�ڵ�E��DF��AC�ڵ�F����ô�ı���CEDF������������˵�����ɣ���ʾ������DG��AB�ڵ�G��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com