
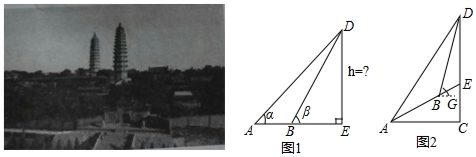
分析 (1)在Rt△ADE中求出AE,在Rt△BDE中求出BE,然后根据AE-BE=AB得出方程,解出即可.
(2)过点B作BG⊥CE于点G,过点D作DH⊥AE,根据图形中的三角函数关系可表示出DH,继而Rt△DEH中可表示出DE.
解答 解:(1)∵在Rt△ABE中,AE=$\frac{DE}{tan∠DAE}$=$\frac{h}{tanα}$,
在Rt△BDE中,BE=$\frac{DE}{tan∠DBE}$=$\frac{h}{tanβ}$,
∴由AE-BE=a可得方程:$\frac{h}{tanα}$-$\frac{h}{tanβ}$=a,
解得:h=$\frac{a•tanα•tanβ}{tanβ-tanα}$,
故答案为:$\frac{h}{tanα}$-$\frac{h}{tanβ}$=a,$\frac{a•tanα•tanβ}{tanβ-tanα}$;
(2)如图,过点B作BG⊥CE于点G,过点D作DH⊥AE,交AE延长线于点H,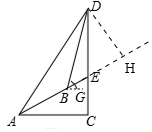
∵tan∠BAC=i=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BAC=30°,
∵∠DAC=60°,
∴∠DAH=∠EAC=30°,
∵∠BGE=∠C=90°,
∴BG∥AC,
∴∠EAC=∠EBG=30°,
∵∠DBG=75°,
∴∠DBH=45°,
由(1)中结论可得:DH=$\frac{AB•tan∠DAH•tan∠DBH}{tan∠DBH-tan∠DAH}$=$\frac{10×\frac{\sqrt{3}}{3}×1}{1-\frac{\sqrt{3}}{3}}$=5$\sqrt{3}$+5,
∵∠BEG=∠DEH、且∠BGE=∠DHE=90°,
∴∠EDH=∠EBG=30°,
∴DE=$\frac{DH}{cos∠EDH}$=$\frac{5\sqrt{3}+5}{\frac{\sqrt{3}}{2}}$=10+$\frac{10}{3}$$\sqrt{3}$,
故塔高为10+$\frac{10}{3}$$\sqrt{3}$米.
点评 本题主要考查解直角三角形的应用-仰角俯角及坡度坡比的问题,熟练掌握三角函数的定义,并添加合适辅助线构建基本模型是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
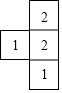 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数,则该几何体的左视图是( )
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数,则该几何体的左视图是( )| A. |  | B. | 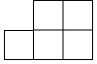 | C. | 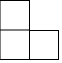 | D. | 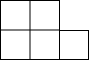 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
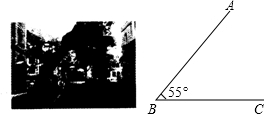 如图,小区内斜向马路的大树与地面的夹角∠ABC为55°,高为3.2米的大型客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米)
如图,小区内斜向马路的大树与地面的夹角∠ABC为55°,高为3.2米的大型客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
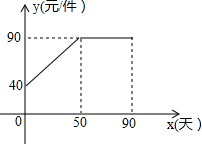 九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如图,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元).
九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如图,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元).| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量 p(件) | 198 | 140 | 80 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
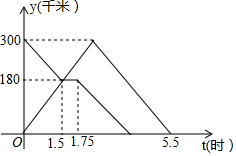 甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地,乙车匀速前往A地,中途与甲车相遇后休息了一会儿,然后以原来的速度继续行驶直到A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时).y与x之间的函数图象如图所示,则乙车到达A地时甲车距B地的路程为150千米.
甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地,乙车匀速前往A地,中途与甲车相遇后休息了一会儿,然后以原来的速度继续行驶直到A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时).y与x之间的函数图象如图所示,则乙车到达A地时甲车距B地的路程为150千米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com