练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    甲是乙现在的年龄时，乙10岁；乙是甲现在的年龄时，甲25岁、那么甲、乙现在的年龄分别为多少岁？请用方程思想解决问题．
    考点：一元一次方程的应用
    专题：
    分析：设甲现在的年龄是x岁，根据已知甲是乙现在的年龄时，乙10岁．乙是甲现在的年龄时，甲25岁，可列方程求解．
    解答：解：甲现在的年龄是x岁，则乙现在的年龄为（2x-25）岁，
    根据题意得：x+10=2（2x-25）
    解得x=20
    2x-25=15岁，
    答：甲现在20岁，乙现在15岁．
    点评：本题考查了一元一次方程的应用，重点考查理解题意的能力，甲、乙年龄无论怎么变，年龄差是不变的．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在?ABCD中，E是CD上的一个动点（不与C、D重合），BE的延长线交AD的延长线于点F，则图中共有
     
    对相似三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线AD对应的函数关系式为y=-x-1，与抛物线交于点A（在x轴上）、点D，抛物线与x轴另一交点为B（3，0），抛物线与y轴交点C（0，-3），
    （1）求抛物线的解析式；
    （2）P是线段AD上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值；
    （3）若点F是抛物线的顶点，点G是直线AD与抛物线对称轴的交点，在线段AD上是否存在一点P，使得四边形GFEP为平行四边形；
    （4）点H抛物线上的动点，在x轴上是否存在点Q，使A、D、H、Q这四个点为顶点的四边形是平行四边形？如果存在，直接写出所有满足条件的Q点坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数y=ax2+（a2-3a-4）x-12a的图象关于y轴对称，并有最大值．
    （1）求此二次函数的解析式，并画出图象．
    （2）若此二次函数与x轴交于点A、B，△ABC为等边三角形（点C在x轴上方），求点C的坐标．
    （3）在此二次函数图象上是否存在点P，使∠APB=60°？若有，请求出点P的坐标；若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

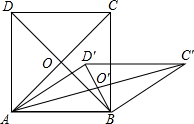    已知正方形ABCD的边长为1，O为其对角线交点，若保持AB不动，将正方形向顺时针方向压扁，得到菱形ABC′D′（如图）．若∠BAD′=30°，则点O运动的路程为（　　）
    A、
    1
    2
    B、
    1
    6
    π
    C、
    		3
    3
    D、
    1
    12
    π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，将△ABC绕顶点A旋转到△ADE处，若∠BAD=40°，则∠ADB的度数是（　　）
    A、50°B、60°
    C、70°D、80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    设关于x的方程x2-4x+（y-1）|x-2|+2-2y=0恰有两个实数根，求y的负整数值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在中央综治委对全国各省市自治区2010年社会治安综合治理考评中，重庆市居全国第一．这跟市政府非常重视交巡警平台的建设有一定关系．据统计，某行政区在去年前7个月内，交巡警平台的数量与月份x之间的关系如下表：
    月份x（月） 1 2 3 4 5 6 7
    交巡警平台数量y1（个） 32 34 36 38 40 42 44
    而由于部分地区陆续被划分到其他行政区，该行政区8月至12月交巡警平台数量y2（个）月份x之间的关系存在如图所示的变化趋势．
    （1）请观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1与x的函数关系式；根据如图的变化趋势，直接写出y2与x的一次函数关系式；
    （2）在2011年内，市政府每月对每一个平台投入用于基础设施、警察报酬等的资金也随月份发生改变，若对每一个平台投入的资金P1（万元）与月份x满足关系式：P1=-0.4x+10（1≤x≤7，且x为整数）；8月至12月的投入的资金P2（万元）与月份x满足关系式：P2=0.2x+12（8≤x≤12，且x为整数）．求去年哪个月政府对该片区的资金投入最大，并求出最大投入的资金．
    （3）2012年1月，政府计划该片区交巡警平台数量比去年12月减少a%，在去年12月的基础上每一个交巡警平台所需的资金将增加0.1a%，某民营企业为表示对平安重庆的鼎力支持，决定在1月对每个交巡警平台赞助30000元．若政府计划1月用于交巡警平台的资金总额为126万元，请参考以下数据，估算a的整数值．（参考数据：872=7569，882=7744，892=7921）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，正方形ABCD的面积设为1，E和F分别是AB和BC的中点，则图中阴影部分的面积是
     
    ．

    查看答案和解析>>

    同步练习册答案