
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
【答案】(1)见解析;(2)成立,见解析;(3)成立,见解析
【解析】
试题分析:(1)从平行线和中点这两个条件出发,延长AE、BC交于点N,如图1(1),易证△ADE≌△NCE,从而有AD=CN,只需证明AM=NM即可.
(2)作FA⊥AE交CB的延长线于点F,易证AM=FM,只需证明FB=DE即可;要证FB=DE,只需证明它们所在的两个三角形全等即可.
(3)在图2(1)中,仿照(1)中的证明思路即可证到AM=AD+MC仍然成立;在图2(2)中,采用反证法,并仿照(2)中的证明思路即可证到AM=DE+BM不成立.
(1)证明:延长AE、BC交于点N,如图1(1),

∵四边形ABCD是正方形,
∴AD∥BC.
∴∠DAE=∠ENC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠ENC=∠MAE.
∴MA=MN.
在△ADE和△NCE中,

∴△ADE≌△NCE(AAS).
∴AD=NC.
∴MA=MN=NC+MC
=AD+MC.
(2)AM=DE+BM成立.
证明:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.

∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.
∵AF⊥AE,
∴∠FAE=90°.
∴∠FAB=90°﹣∠BAE=∠DAE.
在△ABF和△ADE中,

∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM
=∠BAM+∠FAB
=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
(3)①结论AM=AD+MC仍然成立.
证明:延长AE、BC交于点P,如图2(1),
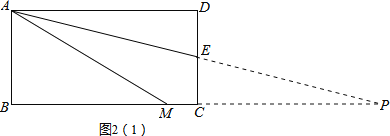
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DAE=∠EPC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠EPC=∠MAE.
∴MA=MP.
在△ADE和△PCE中,

∴△ADE≌△PCE(AAS).
∴AD=PC.
∴MA=MP=PC+MC
=AD+MC.
②结论AM=DE+BM不成立.
证明:假设AM=DE+BM成立.
过点A作AQ⊥AE,交CB的延长线于点Q,如图2(2)所示.

∵四边形ABCD是矩形,
∴∠BAD=∠D=∠ABC=90°,AB∥DC.
∵AQ⊥AE,
∴∠QAE=90°.
∴∠QAB=90°﹣∠BAE=∠DAE.
∴∠Q=90°﹣∠QAB
=90°﹣∠DAE
=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠QAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM
=∠BAM+∠QAB
=∠QAM.
∴∠Q=∠QAM.
∴AM=QM.
∴AM=QB+BM.
∵AM=DE+BM,
∴QB=DE.
在△ABQ和△ADE中,

∴△ABQ≌△ADE(AAS).
∴AB=AD.
与条件“AB≠AD“矛盾,故假设不成立.
∴AM=DE+BM不成立.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】10月18日上午9时,中国共产党第十九次全国代表大会在京开幕,网站PC端成为报道大会的主阵地.据统计,关键词“十九大”在1.3万个网站中产生数据174000条,其中174000用科学记数法表示为( )
A. 17.4×105 B. 1.74×105 C. 17.4×104 D. 1.74×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市荸荠喜获丰收,某生产基地收获荸荠40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润(百元/吨) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在地表以下不太深的地方,温度y(℃)与所处的深度x(km)之间的关系可以近似用关系式y=35x+20表示,这个关系式符合的数学模型是( )
A. 正比例函数 B. 反比例函数 C. 二次函数 D. 一次函数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.

(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′ 、B′ ;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com