
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A.
B.
C.
D.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() ,
,![]() ,
,![]() 为
为![]() 点关于
点关于![]() 的对称点,反比例函数
的对称点,反比例函数![]() 的图像经过
的图像经过![]() 点.
点.

(![]() )证明四边形
)证明四边形![]() 为菱形.
为菱形.
(![]() )求此反比例函数的解析式.
)求此反比例函数的解析式.
(![]() )已知点
)已知点![]() 在
在![]() 的图像上,点
的图像上,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 、
、![]() 、
、![]() 、
、![]() 组成四边形是平行四边形,求
组成四边形是平行四边形,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点.以AD为边在AD的右侧作正方形ADEF.
(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的数量关系为 ;位置关系为 ,
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请举一反例;
(3)设D点坐标为(t,0),当D点从O点运动到C点时,用含t的代数式表示E点坐标,并直接写出E点所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OABC的边OC在x轴的正半轴上,OC=5,反比例函数y= ![]() (x>0)的图象经过点A(1,4).
(x>0)的图象经过点A(1,4).
(1)求反比例函数的关系式和点B的坐标;
(2)如图2,过BC的中点D作DP∥x轴交反比例函数图象于点P,连接AP、OP.
①求△AOP的面积;
②在OABC的边上是否存在点M,使得△POM是以PO为斜边的直角三角形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上). 
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈ ![]() ,cos22°
,cos22° ![]() ,tan22
,tan22 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
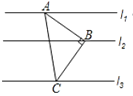
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于F,∠ADC的平分线DG交边AB于G.
(1)线段AF与GB相等吗?
(2)当四边形ABCD满足什么条件时,△EFG为等腰直角三角形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com