
| |||||||||||
(1) |
证法1:(1)因为E为AB的中点,所以AE=EB= 证法2:同证法1,得EB 解题指导:由题目中的条件可以得到△AED和△EBC中三条边相等,或两边及其夹角相等,从而利用“SSS”或“SAS”的判定方法得到△AED≌△EBC |
(2) |
答案:△ACD △ACE △CDE. 解题指导:寻找与△AED的面积相等的三角形要根据△AED的底和高来判断,以AE为底可得△AEC为同底等高的三角形,或△ACD为等底等高的三角形,以ED为底可得△EDC为同底等高的三角形. |


科目:初中数学 来源: 题型:
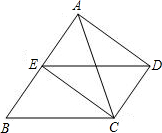 已知,如图,DC∥AB,且DC=
已知,如图,DC∥AB,且DC=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,DC∥AB,DF平分∠CDB,BE平分∠ADB.
已知:如图,DC∥AB,DF平分∠CDB,BE平分∠ADB.| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com