
ЁОЬтФПЁПx2+(p+q)x+pqаЭЪНзгЪЧЪ§бЇбЇЯАжаГЃМћЕФвЛРрЖрЯюЪНЃЌШчКЮНЋетжжРраЭЕФЪНзгвђЪНЗжНтФиЃПвђЮЊ(x+p)(x+q)= x2+(p+q)x+pqЃЌЫљвдЃЌИљОнвђЪНЗжНтЪЧгыећЪНГЫЗЈЗНЯђЯрЗДЕФБфаЮЃЌРћгУетжжЙиЯЕПЩЕУЃКx2+(p+q)x+pq=(x+p)(x+q).ШчЃКx2+3x+2=x2+(1+2)x+1ЁС2=(x+1)(x+2)ЃЌЩЯЪіЙ§ГЬЛЙПЩвдаЮЯѓЕФгУЪЎзжЯрГЫЕФаЮЪНБэЪО:ЯШЗжНтЖўДЮЯюЯЕЪ§ЃЌЗжБ№аДдкЪЎзжНЛВцЯпЕФзѓЩЯНЧКЭзѓЯТНЧЃЛдйЗжНтГЃЪ§ЯюЃЌЗжБ№аДдкЪЎзжНЛВцЯпЕФгвЩЯНЧКЭгвЯТНЧЃЛШЛКѓНЛВцЯрГЫЃЌЧѓДњЪ§КЭЃЌЪЙЦфЕШгквЛДЮЯюЕФЯЕЪ§ЃЌШчЯТЭМ.етбљЃЌЮвУЧПЩвдЕУЕНЃКx2+3x+2= (x+1)(x+2)ЃЌРћгУетжжЗНЗЈЃЌНЋЯТСаЖрЯюЪНЗжНтвђЪНЃК
ЃЈ1ЃЉx2+7x+10
ЃЈ2ЃЉЃ2x2Ѓ6x+36


| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИЪесИЛКЌДѓСПЬњЁЂИЦЁЂаПЕШШЫЬхБиашЕФЮЂСПдЊЫиЃЌЫигаЁАВЙбЊЙћЁБЕФУРГЦЃЌЪЧЖЌМОШШЯњЕФЫЎЙћжЎвЛЃЌЮЊДЫЃЌФГЫЎЙћЩЬМв12дТЗнЕквЛДЮгУ600дЊЙКНјдЦФЯИЪесШєИЩЧЇПЫЃЌЯњЪлЭъКѓЃЌЫћЕкЖўДЮгжгУ600дЊЙКНјИУИЪесЃЌЕЋетДЮУПЧЇПЫЕФНјМлБШЕквЛДЮЕФНјМлЬсИпСЫ20%ЃЌЫљЙКНјИЪесЕФЪ§СПБШЕквЛДЮЩйСЫ25ЧЇПЫЃЎ
ЃЈ1ЃЉЧѓИУЩЬМвЕквЛДЮЙКТђдЦФЯИЪесЕФНјМлЪЧУПЧЇПЫЖрЩйдЊЃП
ЃЈ2ЃЉМйЩшЩЬМвСНДЮЙКНјЕФдЦФЯИЪесАДЭЌвЛМлИёЯњЪлЃЌвЊЪЙЯњЪлКѓЛёРћВЛЕЭгк1000дЊЃЌдђУПЧЇПЫЕФЪлМлжСЩйЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
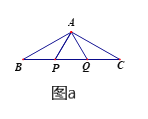
ЁОЬтФПЁПШчЭМЃЌдк7ЁС7ЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЮЊ1ЃЎ
ЃЈ1ЃЉНЈСЂЪЪЕБЕФЦНУцжБНЧзјБъЯЕКѓЃЌШєЕуAЃЈ3ЃЌ4ЃЉЁЂCЃЈ4ЃЌ2ЃЉЃЌдђЕуBЕФзјБъЮЊЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉЭМжаИёЕуЁїABCЕФУцЛ§ЮЊЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
ЃЈ3ЃЉХаЖЯИёЕуЁїABCЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіжЪЕиОљдШЕФаЁе§ЗНЬхЃЌСљИіУцЩЯЗжБ№БъгаЪ§зж1ЃЌ1ЃЌ2ЃЌ4ЃЌ5ЃЌ6ЃЌжРвЛДЮаЁе§ЗНЬхЃЌЙлВьГЏЩЯвЛУцЕФЪ§зжЃЎ
(1)ГЏЩЯЕФЪ§зжЪЧЁА3ЁБЕФЪТМўЪЧЪВУДЪТМўЃПЫќЕФИХТЪЪЧЖрЩйЃП
(2)ГЏЩЯЕФЪ§зжЪЧЁА1ЁБЕФЪТМўЪЧЪВУДЪТМўЃПЫќЕФИХТЪЪЧЖрЩйЃП
(3)ГЏЩЯЕФЪ§зжЪЧХМЪ§ЕФЪТМўЪЧЪВУДЪТМўЃПЫќЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌХзЮяЯп
жаЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЖЅЕуЮЊЕу
ЃЌЖЅЕуЮЊЕу![]() ЃЌЕу
ЃЌЕу![]() гыЕу
гыЕу![]() ЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЃЎ
ЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЃЎ

![]() ЧѓжБЯп
ЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
![]() Еу
Еу![]() дкХзЮяЯпЩЯЃЌЧвЕу
дкХзЮяЯпЩЯЃЌЧвЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЎНЋХзЮяЯпдкЕу
ЃЎНЋХзЮяЯпдкЕу![]() ЃЌ
ЃЌ![]() жЎМфЕФВПЗжЃЈАќКЌЕу
жЎМфЕФВПЗжЃЈАќКЌЕу![]() ЃЌ
ЃЌ![]() ЃЉМЧЮЊЭМЯѓ
ЃЉМЧЮЊЭМЯѓ![]() ЃЌШєЭМЯѓ
ЃЌШєЭМЯѓ![]() ЯђЯТЦНвЦ
ЯђЯТЦНвЦ![]() ИіЕЅЮЛКѓгыжБЯп
ИіЕЅЮЛКѓгыжБЯп![]() жЛгавЛИіЙЋЙВЕуЃЌЧѓ
жЛгавЛИіЙЋЙВЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
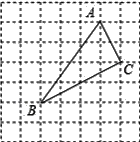
ЁОЬтФПЁПШчЭМaЃЌPЁЂQЪЧЁїABCЕФБпBCЩЯЕФСНЕуЃЌЧвЁїAPQЮЊЕШБпШ§НЧаЮЃЌAB=AC,
ЃЈ1ЃЉЧѓжЄЃКBP=CQ.
ЃЈ2ЃЉШчЭМaЃЌШєЁЯBAC=120![]() ЃЌAP=3ЃЌЧѓBCЕФГЄ.
ЃЌAP=3ЃЌЧѓBCЕФГЄ.
ЃЈ3ЃЉШєЁЯBAC=120![]() ЃЌбижБЯпBCЯђгвЦНаавЦЖЏЁїAPQЕУЕНЁїAЁфPЁфQЁфЃЈШчЭМbЃЉЃЌAЁфQЁфгыACНЛгкЕуM.ЕБЕуPвЦЖЏЕНКЮДІЪБЃЌЁїAAЁфMЁеЁїCQЁфMЃПжЄУїФуЕФНсТл.
ЃЌбижБЯпBCЯђгвЦНаавЦЖЏЁїAPQЕУЕНЁїAЁфPЁфQЁфЃЈШчЭМbЃЉЃЌAЁфQЁфгыACНЛгкЕуM.ЕБЕуPвЦЖЏЕНКЮДІЪБЃЌЁїAAЁфMЁеЁїCQЁфMЃПжЄУїФуЕФНсТл.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯпyЃНkx+kЉ2ОЙ§ЕуЃЈmЃЌn+1ЃЉКЭЃЈm+1ЃЌ2n+3ЃЉЃЌЧвЉ2ЃМkЃМ0ЃЌдђnЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. Љ2ЃМnЃМ0B. Љ4ЃМnЃМЉ2C. Љ4ЃМnЃМ0D. 0ЃМnЃМЉ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЃЌAFЗжБ№ЮЊЁїABCЕФжаЯпКЭИпЃЌBEЮЊЁїABDЕФНЧЦНЗжЯпЃЎ

ЃЈ1ЃЉШєЁЯBED=40ЁуЃЌЁЯBAD=25ЁуЃЌЧѓЁЯBAFЕФДѓаЁЃЛ
ЃЈ2ЃЉШєЁїABCЕФУцЛ§ЮЊ40ЃЌBD=5ЃЌЧѓAFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШчЭМЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЪЧ![]() ЖМдкИёЕуЩЯЃЌ
ЖМдкИёЕуЩЯЃЌ![]() ЖМЪЧаББпдк
ЖМЪЧаББпдк![]() жсЩЯЃЌЧваББпГЄЗжБ№ЮЊ
жсЩЯЃЌЧваББпГЄЗжБ№ЮЊ![]() .ЕФЕШбќжБНЧШ§НЧаЮ.Шє
.ЕФЕШбќжБНЧШ§НЧаЮ.Шє![]() ЕФШ§ИіЖЅЕузјБъЮЊ
ЕФШ§ИіЖЅЕузјБъЮЊ![]() ,дђвРЭМжаЙцТЩ,дђ
,дђвРЭМжаЙцТЩ,дђ![]() ЕФзјБъЮЊ ___________
ЕФзјБъЮЊ ___________

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com