练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

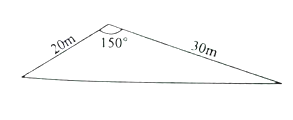
    【题目】我市在旧城改造中，计划在市内一块如下图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价元，则购买这种草皮至少需要______元.

    【答案】150a

    【解析】

    作BA边的高CD，设与BA的延长线交于点D，则∠DAC＝30°，由AC＝30m，即可求出CD＝15m，然后根据三角形的面积公式即可推出△ABC的面积为150m2，最后根据每平方米的售价即可推出结果．

    解：如图，作BA边的高CD，设与BA的延长线交于点D，

    ∵∠BAC＝150°，

    ∴∠DAC＝30°，

    ∵CD⊥BD，AC＝30m，

    ∴CD＝15m，

    ∵AB＝20m，

    ∴S△ABC＝AB×CD＝×20×15＝150m2，

    ∵每平方米售价a元，

    ∴购买这种草皮的价格为150a元．

    故答案为：150a 元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC、连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．

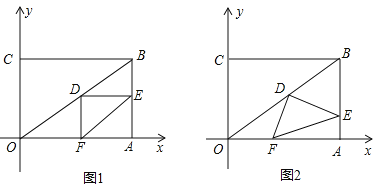
    （1）如图1，当t=3时，求DF的长．

    （2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值．

    （3）连结AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点，点.已知抛物线（是常数），顶点为.

    （Ⅰ）当抛物线经过点时，求顶点的坐标；

    （Ⅱ）若点在轴下方，当时，求抛物线的解析式；

    （Ⅲ） 无论取何值，该抛物线都经过定点.当时，求抛物线的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

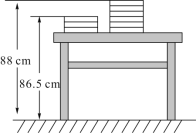
    【题目】新学期开学，两摞规格相同准备发放的数学课本整齐地叠放在讲台上，请根据图中所给的数据信息，解答下列问题：

    (1)一本数学课本的高度是多少厘米？

    (2)讲台的高度是多少厘米？

    (3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示)；

    (4)若桌面上有56本同样的数学课本，整齐叠放成一摞，从中取走18本后，求余下的数学课本距离地面的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，依次作正方形、正方形、…正方形使得点、、…，在直线上，点、、…，在轴上，则点的坐标是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点和点是线段的两个端点，线段，点是点和点的对称中心，点是点和点的对称中心，以此类推，(图中未画出)点是点和点的对称中心．(为正整数)

    （1）填空：线段____________ ；线段_____________ (用含的最简代数式表示)

    （2）试写出线段的长度(用含和的代数式表示，无需说明理由)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某自行车制造厂开发了一款新式自行车，计划6月份生产安装600辆，由于抽调不出足够的熟练工来完成新式自行车的安装，工厂决定招聘一些新工人：他们经过培训后也能独立进行安装．调研部门发现：1名热练工和2名新工人每日可安装8辆自行车；2名熟练工和3名新工人每日可安装14辆自行车．

    （1）每名熟练工和新工人每日分别可以安装多少辆自行车？

    （2）如果工厂招聘n名新工人（0＜n＜10）．使得招聘的新工人和抽调熟练工刚好能完成6月份（30天） 的安装任务，那么工厂有哪几种新工人的招聘方案？

    （3）该自行车关于轮胎的使用有以下说明：本轮胎如安装在前轮，安全行使路程为11千公里；如安装在后轮，安全行使路程为9千公里．请问一对轮胎能行使的最长路程是多少千公里？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校八、九两个年级各有学生180人，为了解这两个年级学生的体质健康情况，进行了抽样调查，过程如下，请补充完整．

    收集数据

    从八、九两个年级各随机抽取名学生，进行了体质健康测试，测试成绩（百分制）如下：

    八年级

    九年级

    整理、描述数据

    按如下分数段整理、描述这两组样本数据：

    八年级

    0

    0

    1

    11

    1

    九年级

    1

    0

    0

    7

    （说明：成绩分及以上为体质健康优秀，~分为体质健康良好，~分为体质健康合格，分以下为体质健康不合格）

    分析数据

    两组样本数据的平均数、中位数、众数、方差如下表所示：

    年级

    平均数

    中位数

    众数

    方差

    八年级

    33.6

    九年级

    52.1

    请将以上两个表格补充完整；

    得出结论

    （1）估计九年级体质健康优秀的学生人数为__________；

    （2）可以推断出_______年级学生的体质健康情况更好一些，理由为_________________．（至少从两个不同的角度说明推断的合理性）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，对角线AC、BD相交于点O，且OA=OB

    （1）求证：四边形ABCD是矩形；

    （2）若AB=5，∠AOB=60°，求BC的长．

    查看答案和解析>>

    同步练习册答案