
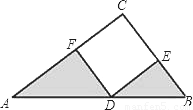
 a,AC=
a,AC= a,在Rt△ABC中,利用勾股定理可得到a2=
a,在Rt△ABC中,利用勾股定理可得到a2= ,再利用三角形的面积公式得S阴影部分=
,再利用三角形的面积公式得S阴影部分= •AE•DE+
•AE•DE+ •DF•BF,代入计算即可得到阴影部分的面积.
•DF•BF,代入计算即可得到阴影部分的面积.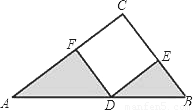
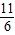 a,AC=
a,AC=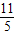 a,
a,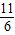 a)2+(
a)2+( 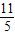 a)2,
a)2,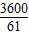 ,
, •AE•DE+
•AE•DE+ •DF•BF
•DF•BF ×(
×(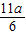 -a)×a+
-a)×a+ ×(
×(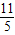 a-a)×a
a-a)×a ×(
×( a2+
a2+ a2)
a2) ×
× ×
×


科目:初中数学 来源: 题型:
 如图,Rt△ADE是由Rt△ABC绕点A顺时针旋转得到的,连接CE交斜边AB于点F,CE 的延长线交BD于点G.
如图,Rt△ADE是由Rt△ABC绕点A顺时针旋转得到的,连接CE交斜边AB于点F,CE 的延长线交BD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•黄埔区一模)
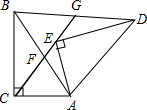
(2013•黄埔区一模)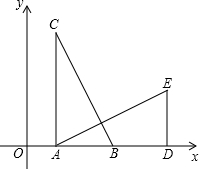 如图,Rt△ADE可由Rt△CAB旋转而成,点B的对应点是E,点A的对应点是D,点B、C的坐标分别为(3,0),(1,4).
如图,Rt△ADE可由Rt△CAB旋转而成,点B的对应点是E,点A的对应点是D,点B、C的坐标分别为(3,0),(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:
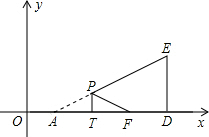
如图![]() ,Rt△ADE≌ Rt△BEC, ∠A =∠B =90°,使A、E、B在 同一直线上,连结CD.
,Rt△ADE≌ Rt△BEC, ∠A =∠B =90°,使A、E、B在 同一直线上,连结CD.
(1)求证:∠1 =∠2 =45°
(2)若AD =3,AB =7,请求出△ECD的面积.
(3)若P为CD的中点,连结PA、PB。试判断△APB的形状,并证明之。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com