
【题目】如图1,∠AOB=90°,OA=4,OB=3,点E在线段OA上,EP⊥OA交AB于点N,PM⊥AB,直线PB与AO交于点F.
(1)若AN=3,S△PBN=8,求PN的长;
(2)设△PMN的周长为C1,△AEN的周长为C2,若△PFE~△BAO且![]() =
=![]() ,求OE的长;
,求OE的长;
(3)如图2,若OE=2,将线段OE绕点O逆时针旋转得到OE',旋转角为α (0°<α<90°),连接E'A、E'B,求E'A+![]() E'B的最小值.
E'B的最小值.

【答案】(1)PN=10;(2)OE=![]() ;(3)
;(3)![]()
【解析】
(1)证明△PMN∽△AOB,可得![]() ,由此即可解决问题.
,由此即可解决问题.
(2)如图1﹣2中,作BK⊥PN于K,设PN=6k.利用等腰三角形的性质证明PK=KN=3k,BK=4k,BN=5k,由△PMN∽△AEN,且![]() ,推出
,推出![]() ,推出AN=10k,可得AB=15k=5,解得k=
,推出AN=10k,可得AB=15k=5,解得k=![]() ,由此即可解决问题.
,由此即可解决问题.
(3)如图3中,在BO上取一点的K,使得OK=![]() ,连接KE′,KA.证明△OKE′∽△OE′B,推出E′K:BE′=OE′:OB=2:3,推出E′K=
,连接KE′,KA.证明△OKE′∽△OE′B,推出E′K:BE′=OE′:OB=2:3,推出E′K=![]() BE′,推出AE′+
BE′,推出AE′+![]() BE′=AE′+KE′,由AE′+KE′≥AK,求出AK即可解决问题.
BE′=AE′+KE′,由AE′+KE′≥AK,求出AK即可解决问题.
解:(1)如图1﹣1中,
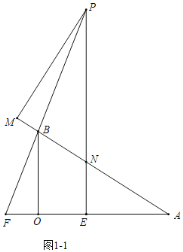
在Rt△AOB中,∵OB=3,OA=4,
∴AB=![]() ,
,
∵AN=3,
∴BN=AB﹣AN=2,
∵PM⊥AM,
∴S△PBN=![]() =8,
=8,
∴PM=8,
∵PE⊥OA,
∴∠AEN=∠AOB=∠M=90°,
∴OB∥PN,
∴∠ABO=∠PNM,
∴△PMN∽△AOB,
∴![]() ,
,
∴![]() ,
,
∴PN=10.
(2)如图1﹣2中,作BK⊥PN于K,设PN=6k.
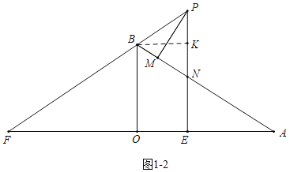
∵△PFE∽△BAO,
∴∠F=∠A,
∵PK∥AF,
∴∠PBK=∠∠KBN=∠A,
∴∠PBK=∠KBN,
∵BK⊥PN,
∴∠BKP=∠BKN=90°,
∴∠BPK+∠PBK=90°,∠BNK+∠KBN=90°,
∴∠BPK=∠BNK,
∴BP=BN,
∴PK=KN=3k,BK=4k,BN=5k,
∵△PMN∽△AEN,且![]() ,
,
∴![]() ,
,
∴AN=10k,
∴AB=15k=5,
∴k=![]() ,
,
∴BK=![]() ,
,
∵四边形BOEK是矩形,
∴OE=BK=![]() .
.
(3)如图3中,在BO上取一点的K,使得OK=![]() ,连接KE′,KA.
,连接KE′,KA.
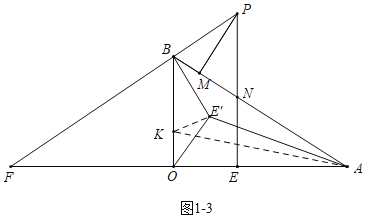
∵OE′2=4,OKOB=![]() ×3=4,
×3=4,
∴OE′2=OKOB,
∴![]() ,
,
∵∠KOE′=∠BOE′,
∴△OKE′∽△OE′B,
∴E′K:BE′=OE′:OB=2:3,
∴E′K=![]() BE′,
BE′,
∴AE′+![]() BE′=AE′+KE′,
BE′=AE′+KE′,
∵AE′+KE′≥AK,AK=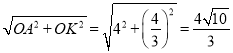 ,
,
∴AE′+![]() BE′≥
BE′≥![]() ,
,
∴E'A+![]() E'B的最小值为
E'B的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(![]() ,3),B(
,3),B(![]() ,2),C(0,
,2),C(0,![]() ).
).
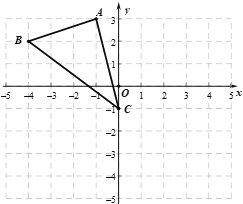
(1)以y轴为对称轴,把△ABC沿y轴翻折,画出翻折后的△![]() ;
;
(2)在(1)的基础上,
①以点C为旋转中心,把△![]() 顺时针旋转90°,画出旋转后的△
顺时针旋转90°,画出旋转后的△![]() ;
;
②点![]() 的坐标为 ,在旋转过程中点
的坐标为 ,在旋转过程中点![]() 经过的路径
经过的路径![]() 的长度为_____(结果保留π).
的长度为_____(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:
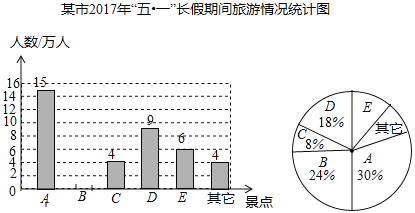
(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为5的正方形ABCD中,点E在BC边上,连接AE,过D作DF//AE交BC的延长线于点F,过点C作CG⊥DF于点G,延长AE、GC交于点H,点P是线段DG上的任意一点(不与点D、点G重合),连接CP,将△CPG沿CP翻折得到![]() ,连接
,连接![]() . 若CH=1,则
. 若CH=1,则![]() 长度的最小值为__________.
长度的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围.
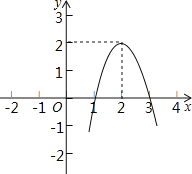
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有完全相同的三个小球,把它们分别标号为1,2,3. 小林和小华做一个游戏,按照以下方式抽取小球:先从布袋中随机抽取一个小球,记下标号后放回布袋中搅匀,再从布袋中随机抽取一个小球, 记下标号. 若两次抽取的小球标号之和为奇数,小林赢;若标号之和为偶数,则小华赢.
(1)用画树状图或列表的方法,列出前后两次取出小球上所标数字的所有可能情况;
(2)请判断这个游戏是否公平,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
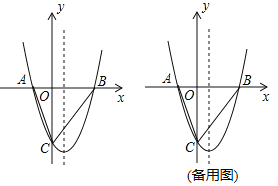
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于C点,OA=2,OC=6,连接AC和BC.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,当△ACD的周长最小时,求点D的坐标;
(3)点E是第四象限内抛物线上的动点,连接CE和BE.求△BCE面积的最大值及此时点E的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com