
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
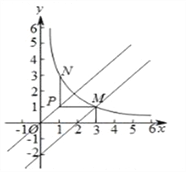
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交函数
轴的直线,交函数![]() 的图象于点
的图象于点![]() .
.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
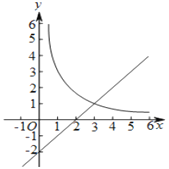
【答案】(1)k=3,m= 1;(2)①PM=PN,②0<n≤1或n≥3
【解析】分析:(1)将A点代入y=x-2中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值.
(2)①当n=1时,分别求出M、N两点的坐标即可求出PM与PN的关系;
②由题意可知:P的坐标为(n,n),由于PN≥PM,从而可知PN≥2,根据图象可求出n的范围.
详解:(1)将A(3,m)代入y=x-2,
∴m=3-2=1,
∴A(3,1),
将A(3,1)代入y=![]() ,
,
∴k=3×1=3,
m的值为1.
(2)①当n=1时,P(1,1),
令y=1,代入y=x-2,
x-2=1,
∴x=3,
∴M(3,1),
∴PM=2,
令x=1代入y=![]() ,
,
∴y=3,
∴N(1,3),
∴PN=2
∴PM=PN,
②P(n,n),
点P在直线y=x上,
过点P作平行于x轴的直线,交直线y=x-2于点M,
M(n+2,n),
∴PM=2,
∵PN≥PM,
即PN≥2,
∴0<n≤1或n≥3


科目:初中数学 来源: 题型:
【题目】下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;
⑤若![]() 的弦AB,CD交于点P,则
的弦AB,CD交于点P,则![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:
①CF=AE;②OE=OF;③图中共有四对全等三角形;④四边形ABCD是平行四边形;其中正确结论的是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)当a=2,b=![]() 时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值;
时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值;
(2)当a=﹣5,b=﹣3时,a2﹣2ab+b2 (a﹣b)2(填“=“,“<”“>”)
(3)观察(1)(2)中代探索代数式a2﹣2ab+b2和(a﹣b)2有何数量关系,并把探索的结果写出来:a2﹣2ab+b2 (a﹣b)2(填“=”,“<”“>”)
(4)利用你发现的规律,求135.72﹣2×135.7×35.7+35.72的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对[Q,R]的好点.
根据下列题意解答问题:
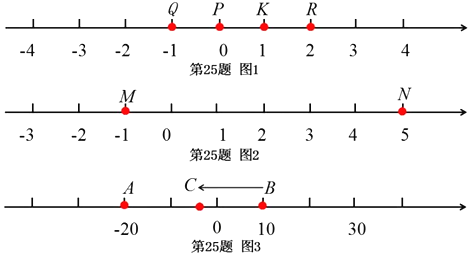
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R
表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是
有序点对![]() 的好点,但点K不是有序点对
的好点,但点K不是有序点对![]() 的好点.同理可以判断:
的好点.同理可以判断:
点P__________有序点对![]() 的好点,点R______________有序点对
的好点,点R______________有序点对![]() 的好点(填“是”或“不是”);
的好点(填“是”或“不是”);
(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,若点X是有序点对![]() 的好点,求点X所表示的数,并说明理由?
的好点,求点X所表示的数,并说明理由?
(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从
点B出发,以每秒2个单位的速度向左运动t秒.当点A、B、C中恰有一个点为其余两有序点对的好点,求t的所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
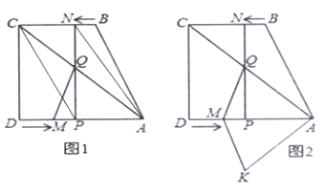
【题目】如图1,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
(1)连接![]() 、
、![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(2)求出点![]() 到
到![]() 的距离;
的距离;
(3)如图2,将![]() 沿
沿![]() 翻折,得
翻折,得![]() ,是否存在某时刻
,是否存在某时刻![]() ,使四边形
,使四边形![]() 为菱形,若存在,求
为菱形,若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)判断BE与CF的数量关系,并说明理由;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连OB,将纸片OABC沿OB折叠,使点A落在A′的位置,若OB=![]() ,tan∠BOC=
,tan∠BOC=![]() ,则点A′的坐标( )
,则点A′的坐标( )

A. (![]() ,
,![]() ) B. (﹣
) B. (﹣![]() ,
,![]() ) C. (﹣
) C. (﹣![]() ,
,![]() ) D. (﹣
) D. (﹣![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com