
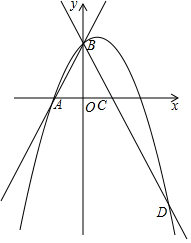
 ČēĶ¼£¬Ö±Ļßy=2x+2ÓėxÖį½»ÓŚµćA£¬Óė yÖį½»ÓŚµćB£¬°Ń”÷AOBŃŲyÖį·Īö£¬µćAĀäµ½Cµć£¬¹żµćBµÄÅ×ĪļĻßy=-x2+bx+cÓėÖ±ĻßBC½»ÓŚµćD£Ø3£¬-4£©£®
ČēĶ¼£¬Ö±Ļßy=2x+2ÓėxÖį½»ÓŚµćA£¬Óė yÖį½»ÓŚµćB£¬°Ń”÷AOBŃŲyÖį·Īö£¬µćAĀäµ½Cµć£¬¹żµćBµÄÅ×ĪļĻßy=-x2+bx+cÓėÖ±ĻßBC½»ÓŚµćD£Ø3£¬-4£©£®·ÖĪö £Ø1£©ÓÉÖ±Ļßy=2x+2æÉŅŌĒó³öA£¬BµÄ×ų±ź£¬ÓÉ“ż¶ØĻµŹż·Ø¾ĶæÉŅŌĒó³öÅ×ĪļĻߵĽāĪöŹ½ŗĶÖ±ĻßBDµÄ½āĪöŹ½£»
£Ø2£©ČēĶ¼1£¬2£¬ÓÉ£Ø1£©µÄ½āĪöŹ½ÉčM£Øa£¬-a2+a+2£©£¬µ±”÷BOC”×”÷MON»ņ”÷BOC”×”÷ONMŹ±£¬ÓÉĻąĖĘČż½ĒŠĪµÄŠŌÖŹ¾ĶæÉŅŌĒó³ö½įĀŪ£»
£Ø3£©ÉčP£Øb£¬-b2+b+2£©£¬H£Øb£¬-2b+2£©£®ÓÉĘ½ŠŠĖıߊĪµÄŠŌÖŹ½ØĮ¢·½³ĢĒó³öbµÄÖµ¾ĶæÉŅŌĒó³ö½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©”ßy=2x+2£¬
”ąµ±x=0Ź±£¬y=2£¬
”ąB£Ø0£¬2£©£®
µ±y=0Ź±£¬x=-1£¬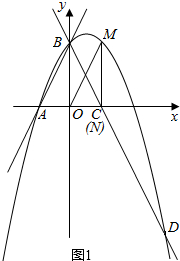
”ąA£Ø-1£¬0£©£®
”ßÅ×ĪļĻßy=-x2+bx+c¹żµćB£Ø0£¬2£©£¬D£Ø3£¬-4£©£¬
”ą$\left\{\begin{array}{l}{2=c}\\{-4=-9+3b+c}\end{array}\right.$
½āµĆ£ŗ$\left\{\begin{array}{l}{b=1}\\{c=2}\end{array}\right.$£¬
”ąy=-x2+x+2£»
ÉčÖ±ĻßBDµÄ½āĪöŹ½ĪŖy=kx+b£¬ÓÉĢāŅā£¬µĆ
$\left\{\begin{array}{l}{b=2}\\{-4=3k+b}\end{array}\right.$£¬
½āµĆ£ŗ$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$£¬
”ąÖ±ĻßBDµÄ½āĪöŹ½ĪŖ£ŗy=-2x+2£»
£Ø2£©“ęŌŚ£®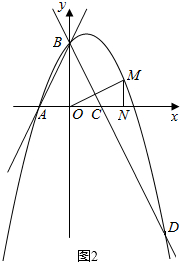
ČēĶ¼1£¬ÉčM£Øa£¬-a2+a+2£©£®
”ßMN“¹Ö±ÓŚxÖį£¬
”ąMN=-a2+a+2£¬ON=a£®
”ßy=-2x+2£¬
”ąy=0Ź±£¬x=1£¬
”ąC£Ø1£¬0£©£¬
”ąOC=1£®
”ßB£Ø0£¬2£©£¬
”ąOB=2£®
µ±”÷BOC”×”÷MNOŹ±£¬
”ą$\frac{BO}{MN}$=$\frac{OC}{ON}$£¬
”ą$\frac{2}{-{a}^{2}+a+2}$=$\frac{1}{a}$£¬
½āµĆ£ŗa1=1£¬a2=-2£ØÉįČ„£©
”ąM£Ø1£¬2£©£»
ČēĶ¼2£¬µ±”÷BOC”×”÷ONMŹ±£¬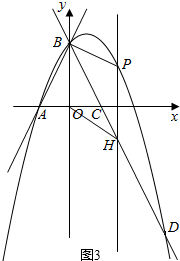
$\frac{BO}{ON}$=$\frac{OC}{MN}$£¬
”ą$\frac{2}{a}$=$\frac{1}{-{a}^{2}+a+2}$£¬
”ąa=$\frac{1+\sqrt{33}}{4}$»ņ$\frac{1-\sqrt{33}}{4}$£ØÉįČ„£©£¬
”ąM£Ø$\frac{1+\sqrt{33}}{4}$£¬$\frac{1+\sqrt{33}}{8}$£©£®
”ą·ūŗĻĢõ¼žµÄµćMµÄ×ų±źĪŖ£Ø1£¬2£©£¬£Ø$\frac{1+\sqrt{33}}{4}$£¬$\frac{1+\sqrt{33}}{8}$£©£»
£Ø3£©ÉčP£Øb£¬-b2+b+2£©£¬H£Øb£¬-2b+2£©£®
ČēĶ¼3£¬”ßĖıߊĪBOHPŹĒĘ½ŠŠĖıߊĪ£¬
”ąBO=PH=2£®
”ßPH=-b2+b+2+2b-2=-b2+3b£®
”ą2=-b2+3b
”ąb1=1£¬b2=2£®
µ±b=1Ź±£¬P£Ø1£¬2£©£¬
µ±b=2Ź±£¬P£Ø2£¬0£©
”ąPµćµÄ×ų±źĪŖ£Ø1£¬2£©»ņ£Ø2£¬0£©£®
µćĘĄ ±¾Ģāæ¼²éĮĖ“ż¶ØĻµŹż·ØĒ󶞓ĪŗÆŹżµÄ½āĪöŹ½£¬Ņ»“ĪŗÆŹżµÄ½āĪöŹ½µÄŌĖÓĆ£¬ĻąĖĘČż½ĒŠĪµÄŠŌÖŹµÄŌĖÓĆ£¬Ę½ŠŠĖıߊĪµÄŠŌÖŹµÄŌĖÓĆ£¬Ņ»ŌŖ¶ž“Ī·½³ĢµÄ½ā·ØµÄŌĖÓĆ£¬½ā“šŹ±Ēó³öŗÆŹżµÄ½āĪöŹ½ŹĒ¹Ų¼ü£®


 ¾ŁŅ»·“ČżĶ¬²½Ēɽ²¾«Į·ĻµĮŠ“š°ø
¾ŁŅ»·“ČżĶ¬²½Ēɽ²¾«Į·ĻµĮŠ“š°ø æŚĖćÓėÓ¦ÓĆĢāæØĻµĮŠ“š°ø
æŚĖćÓėÓ¦ÓĆĢāæØĻµĮŠ“š°ø ĆūŹ¦µć¾¦×Ö“Ź¾ä¶ĪĘŖĻµĮŠ“š°ø
ĆūŹ¦µć¾¦×Ö“Ź¾ä¶ĪĘŖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
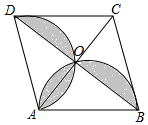 ČēĶ¼£¬ĮāŠĪABCDµÄ¶Ō½ĒĻßAC£¬BDĻą½»ÓŚµćO£¬AC=6£¬BD=8£¬·Ö±šŅŌAB”¢ADĪŖÖ±¾¶×÷Ņ»øö°ėŌ²£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ£Ø””””£©
ČēĶ¼£¬ĮāŠĪABCDµÄ¶Ō½ĒĻßAC£¬BDĻą½»ÓŚµćO£¬AC=6£¬BD=8£¬·Ö±šŅŌAB”¢ADĪŖÖ±¾¶×÷Ņ»øö°ėŌ²£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ£Ø””””£©| A£® | $\frac{25}{4}$¦Š-12 | B£® | $\frac{16}{3}$¦Š-3 | C£® | $\frac{9}{2}$¦Š-6 | D£® | $\frac{25}{8}$¦Š-6 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
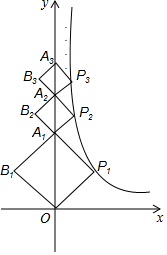 ČēĶ¼£¬ĖıߊĪOP1A1B1”¢A1P2A2B2”¢A2P3A3B3”¢””¢An-1PnAnBn¶¼ŹĒÕż·½ŠĪ£¬¶Ō½ĒĻßOA1”¢A1A2”¢A2A3”¢””¢An-1An¶¼ŌŚyÖįÉĻ£Øn”Ż1µÄÕūŹż£©£¬µćP1£Øx1£¬y1£©£¬µćP2£Øx2£¬y2£©£¬”£¬Pn£Øxn£¬yn£©ŌŚ·“±ČĄżŗÆŹży=$\frac{k}{x}$£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬²¢ŅŃÖŖB1£Ø-1£¬1£©£®
ČēĶ¼£¬ĖıߊĪOP1A1B1”¢A1P2A2B2”¢A2P3A3B3”¢””¢An-1PnAnBn¶¼ŹĒÕż·½ŠĪ£¬¶Ō½ĒĻßOA1”¢A1A2”¢A2A3”¢””¢An-1An¶¼ŌŚyÖįÉĻ£Øn”Ż1µÄÕūŹż£©£¬µćP1£Øx1£¬y1£©£¬µćP2£Øx2£¬y2£©£¬”£¬Pn£Øxn£¬yn£©ŌŚ·“±ČĄżŗÆŹży=$\frac{k}{x}$£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬²¢ŅŃÖŖB1£Ø-1£¬1£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® |  | B£® |  | C£® | 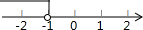 | D£® | 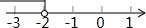 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
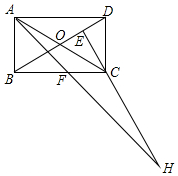 ŌŚ¾ŲŠĪABCDÖŠ£¬AB=1£¬AD=$\sqrt{3}$£¬AFĘ½·Ö”ĻDAB£¬¹żCµć×÷CE”ĶBDÓŚE£¬ŃÓ³¤AFÓėEC½»ÓŚµćH£¬ĻĀĮŠ½įĀŪÖŠ£ŗ¢ŁAF=FH£»¢ŚBO=BF£»¢ŪAC=HC£»¢ÜBE=3DE£¬ÕżČ·µÄŹĒ£Ø””””£©
ŌŚ¾ŲŠĪABCDÖŠ£¬AB=1£¬AD=$\sqrt{3}$£¬AFĘ½·Ö”ĻDAB£¬¹żCµć×÷CE”ĶBDÓŚE£¬ŃÓ³¤AFÓėEC½»ÓŚµćH£¬ĻĀĮŠ½įĀŪÖŠ£ŗ¢ŁAF=FH£»¢ŚBO=BF£»¢ŪAC=HC£»¢ÜBE=3DE£¬ÕżČ·µÄŹĒ£Ø””””£©| A£® | ¢Ś¢Ü | B£® | ¢Ū¢Ü | C£® | ¢Ś¢Ū¢Ü | D£® | ¢Ł¢Ś¢Ū¢Ü |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com