
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
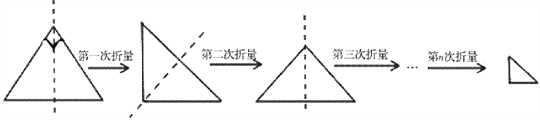
图1 图2 图3 图n+1
科目:初中数学 来源: 题型:
【题目】根据绝对值定义,若有![]() ,则
,则![]() 或
或![]() ,若
,若![]() ,则
,则![]() ,我们可以根据这样的结论,解一些简单的绝对值方程,例如:
,我们可以根据这样的结论,解一些简单的绝对值方程,例如:![]()
解:方程![]() 可化为:
可化为:
![]() 或
或![]()
当![]() 时, 则有:
时, 则有:![]() ; 所以
; 所以 ![]() .
.
当![]() 时, 则有:
时, 则有:![]() ;所以
;所以 ![]() .
.
故,方程![]() 的解为
的解为![]() 或
或![]() 。
。
(1)解方程:![]()
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)在 (2)的条件下,若![]() 都是整数,则
都是整数,则![]() 的最大值是 (直接写结果,不需要过程).
的最大值是 (直接写结果,不需要过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】缴纳个人所得税是收入达到缴纳标准的公民应居的义务,个人所得税率是由国家相应的法律法规规定的.根据个人的收入计算,新修改的《中华人民共和国个人所得税法》于2019年1月1日正式实施,新税法规定个人所得税的免征额为5000元,应纳税所得额按如下税率表缴纳个人所得税(应纳税所得额=税前收总额﹣国家规定扣除专项金额﹣免征额).
级数 | 应纳税所得额 | 税率% |
1 | 不超过3000元的 | 3 |
2 | 超过3000元至12000元的部分 | 10 |
3 | 超过12000元至25000元的部分 | 20 |
… | … | … |
根据以上信息,解决以下问题:
(1)小明的妈妈应纳税所得额为2000元,她应该缴纳个人所得税______元.
(2)小明的爸爸要缴纳个人所得税590元,他应纳税所得额是多少元?
(3)如果小明的爸爸和妈妈某月应纳税所得额共为20000元(爸爸的应纳税所得额高于妈妈的应纳税所得额),共要缴纳个人所得税1780元,小明的爸爸应纳税所得额是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“完美数”。例如5是“完美数”,因为5=22+12,再如M=x2+2xy+2y2=(x+y)2 +y2(x、y是正整数),所以M也是“完美数”。
(1)请你再写一个小于10的“完美数”,并判断29是否为“完美数”;
(2)试判断(x2+9y2)(4y2+x2)(x、y是正整数)是否为“完美数”,并说明理由;
(3)已知S=x2+4y2+4x-12y+k(x、y是正整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数小1,那么我们把这样的自然数叫做“相连数”,例如:234,4567,56789,......都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的和;
(2)若某个“相连数”恰好等于其个位数的576倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在![]() 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校![]() 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
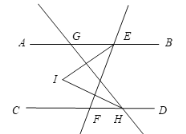
【题目】如图1,直线AB∥CD,直线EF交AB于点E,交CD于点F,点G和点H分别是直线AB和CD上的动点,作直线GH,EI平分∠AEF,HI平分∠CHG,EI与HI交于点I.
(1)如图,点G在点E的左侧,点H在点F的右侧,若∠AEF=70°,∠CHG=60°,求∠ETH的度数.
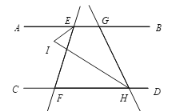
(2)如图,点G在点E的右侧,点H也在点F的右侧,若∠AEF=![]() ,∠CHG=β,其他条件不变,求∠ETH的度数.
,∠CHG=β,其他条件不变,求∠ETH的度数.
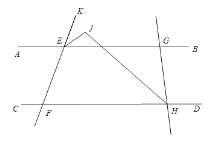
(3)如图,点G在点E的右侧,点H也在点F的右侧,∠GHC的平分线HJ交∠KEG的平分线EJ于点J.其他条件不变,若∠AEF=![]() ,∠CHG=β,求∠EJH的度数.
,∠CHG=β,求∠EJH的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com