
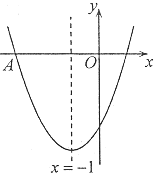
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(-3,0),其对称轴为直线x=-1,有下列结论:①abc<0;②a-b-2c>0;③关于![]() 的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若
的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若![]() ,
,![]() 是抛物线上两点,且
是抛物线上两点,且![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据抛物线开口方向、对称轴、及与y轴的交点位置可对①进行判断;根据对称轴和抛物线与x的一个交点(-3,0)可得另一个交点坐标为(1,0),可知![]() =-3,即c=-3a,根据对称轴方程可得b=2a,代入a-b-2c,根据a的符号即可对②进行判断;根据b2-4ac>0,b=2a,判断方程ax2+(b-m)x+c=m的判别式的符号即可对③进行判断;把P、Q两点坐标代入抛物线解析式,根据y1>y2列出不等式,根据c=-3a,b=2a解不等式求出m的取值范围即可对④进行判断.
=-3,即c=-3a,根据对称轴方程可得b=2a,代入a-b-2c,根据a的符号即可对②进行判断;根据b2-4ac>0,b=2a,判断方程ax2+(b-m)x+c=m的判别式的符号即可对③进行判断;把P、Q两点坐标代入抛物线解析式,根据y1>y2列出不等式,根据c=-3a,b=2a解不等式求出m的取值范围即可对④进行判断.
∵抛物线开口向上,与y轴交点在y轴负半轴,
∴a>0,c<0,
∵对称轴x=![]() =-1<0,
=-1<0,
∴b>0,b=2a,
∴abc<0,故①正确,
∵对称轴为x=-1,与x轴的一个交点为A(-3,0),
∴抛物线与x轴的另一个交点为(1,0),
∴![]() =-3,即c=-3a,
=-3,即c=-3a,
∴a-b-2c=a-2a+6a=5a>0,故②正确,
方程ax2+(b-m)x+c=m的判别式为△=(b-m)2-4a(c-m)=b2-4ac+m2-2m(b-2a)
∵抛物线y=ax2+bx+c与x轴有两个交点,
∴b2-4ac>0,
∵b=2a,
∴△= b2-4ac+m2>0,
∴方程ax2+(b-m)x+c=m有两个不相等的实数根,故③正确,
∵P(-5,y1)、Q(m,y2)是抛物线上两点,
∴y1=25a-5b+c,y2=am2+bm+c,
∵y1>y2,
∴25a-5b>am2+bm,
∵b=2a,
∴25a-10a>am2+2am,
∵a>0,
∴m2+2m-15<0,
解得:-5<m<3,故④正确,
综上所述:正确的结论有①②③④,共4个,
故选D.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
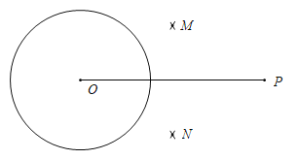
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
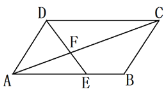
【题目】如图,在□ABCD中,点E是AB上一点,且AE=2EB .
(1)求![]() 的值.
的值.
(2)求![]() 的值.
的值.
(3)如果△AEF的面积![]() =8cm2,分别求出△CDF的面积
=8cm2,分别求出△CDF的面积![]() 和△ADF的面积
和△ADF的面积![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
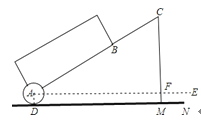
【题目】一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,点B距离水平面38cm,点C距离水平面59cm.
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
查看答案和解析>>
科目:初中数学 来源: 题型:
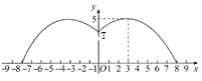
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利川市南门大桥是上世纪90年代修建的一座石拱桥,其主桥孔的横截面是一条抛物线的一部分,2019年在维修时,施工队测得主桥孔最高点![]() 到水平线
到水平线![]() 的高度为
的高度为![]() .宽度
.宽度![]() 为
为![]() .如图所示,现以
.如图所示,现以![]() 点为原点,
点为原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
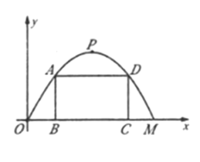
(1)直接写出点![]() 及抛物线顶点
及抛物线顶点![]() 的坐标;
的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在主桥孔内搭建矩形“脚手架”![]() ,使
,使![]() 点在抛物线上,
点在抛物线上,![]() 点在水平线
点在水平线![]() 上,为了筹备材料,需求出“脚手架”三根钢管
上,为了筹备材料,需求出“脚手架”三根钢管![]() 的长度之和的最大值是多少?请你帮施工队计算.
的长度之和的最大值是多少?请你帮施工队计算.
查看答案和解析>>
科目:初中数学 来源: 题型:
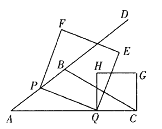
【题目】如图,在![]() 中,
中,![]() =5,
=5,![]() =9,
=9,![]() =
=![]() ,动点
,动点![]() 从
从![]() 出发,沿射线
出发,沿射线![]() 方向以每秒5个单位长度的速度运动,动点
方向以每秒5个单位长度的速度运动,动点![]() 从
从![]() 点出发,一相同的速度在线段
点出发,一相同的速度在线段![]() 上由
上由![]() 向
向![]() 运动,当
运动,当![]() 点运动到
点运动到![]() 点时,
点时,![]() 两点同时停止运动,以
两点同时停止运动,以![]() 为边作正方形
为边作正方形![]() (
(![]() 按逆时针排序),以
按逆时针排序),以![]() 为边在
为边在![]() 上方作正方形
上方作正方形![]() .
.
(1)![]() _______.
_______.
(2)设点![]() 运动时间为
运动时间为![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,请探究
,请探究![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
(3)当![]() 为何值时,正方形
为何值时,正方形![]() 的某个顶点(
的某个顶点(![]() 点除外)落在正方形
点除外)落在正方形![]() 的边
的边![]() 上,请直接写出
上,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+3经过点A(﹣1,8),顶点为M;
(1)求抛物线的表达式;
(2)设抛物线对称轴与x轴交于点B,连接AB、AM,求△ABM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com