
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( ) 
A.①②
B.②③
C.①③
D.①④
【答案】D
【解析】解:∵AE= ![]() AB, ∴BE=2AE,
AB, ∴BE=2AE,
由翻折的性质得,PE=BE,
∴∠APE=30°,
∴∠AEP=90°﹣30°=60°,
∴∠BEF= ![]() (180°﹣∠AEP)=
(180°﹣∠AEP)= ![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴∠EFB=90°﹣60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,
∴EF=2PE,
∵EF>PF,
∴PF<2PE,故②错误;
由翻折可知EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质,∠EFB=∠EFP=30°,
∴∠BFP=30°+30°=60°,
∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,
∴∠PBF=∠PFB=60°,
∴△PBF是等边三角形,故④正确;
综上所述,结论正确的是①④.
故选:D.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点M在抛物线y=(x﹣3)2﹣4的对称轴上,则点M的坐标可能是( )
A.(1,0)B.(3,5)C.(﹣3,﹣4)D.(0,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
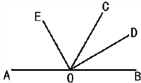
【题目】如图,点O在直线AB上,OE、OD分别是∠AOC、∠BOC的平分线.
(1)∠AOE的补角是∠____;∠BOD的余角是______;
(2)若∠AOC=118°,求∠COD的度数;
(3)射线OD与OE之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为-1.
时,该代数式的值为-1.
(1)求![]() 的值。
的值。
(2)已知当![]() 时,该代数式的值为-1,求
时,该代数式的值为-1,求![]() 的值。
的值。
(3)已知当![]() 时,该代数式的值为9,试求当
时,该代数式的值为9,试求当![]() 时该代数式的值。
时该代数式的值。
(4)在第(3)小题已知条件下,若有![]() 成立,试比较
成立,试比较![]() 与
与![]() 的大小。
的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在△ABC中,点O是∠ABC和∠ACB的平分线的交点,若∠A=α,则∠BOC=90°+![]() ;如图②,∠CBO=
;如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC=__________(用α表示);
∠ACB,∠A=α,则∠BOC=__________(用α表示);
(2)如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC=__________(用α表示).
∠ECB,∠A=α,请猜想∠BOC=__________(用α表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式:__________________________;
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图③中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)琪琪用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 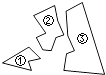
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com