
分析 (1)将x=1000代入y=-0.01x+150,即可解答本题;
(2)根据题意可以分别表示出w内,w外与x之间的函数关系式;
(3)将x=5000分别代入(2)中的解析式,然后讨论a的取值范围,即可解答本题.
解答 解:(1)当x=1000时,y=-0.01×1000+150=140,
故答案为:140;
(2)由题意可得,
W内=x(y-20)-62500=x(-0.01x+150-20)-62500=-0.01x2+130x-62500,
W外=-0.01x2+x (150-a);
(3)当x=5000时,W内=337500,W外=-5000a+500000,
若W内<W外,则a<32.5;即当10≤a<32.5时,选择在国外销售,
若W内=W外,则a=32.5;即当a=32.5时,在国外和国内销售一样,
若W内>W外,则a>32.5;即当32.5<a≤40时,选择在国内销售.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
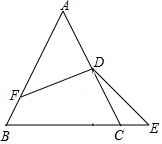 已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.
已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=0.5x2-3.5x-4经过A、B两点.若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连结PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积.
如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=0.5x2-3.5x-4经过A、B两点.若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连结PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sin20°<sin40°<sin70° | B. | cos20°<cos40°<cos70° | ||
| C. | tan20°<tan40°<tan70° | D. | sin30°<cos45°<tan60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
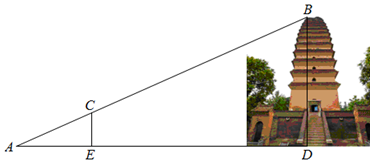
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com