
如图,抛物线y =ax2+bx+c过点A(-1,0),且经过直线y =x-3与x轴 的交点B及与y轴的交点C.
的交点B及与y轴的交点C.
【小题1】(1)求点B、C的坐标;
【小题2】(2)求抛物线的解析式;
【小题3】(3)求抛物线的顶点M的坐标;
【小题4】(4)在直线y =x-3上是否存在点P,使△CMP是等腰三角形?若存在,求出满足条件的P点坐标;若不存在,说明理由.
【小题1】解:(1)在y =x-3中,分别令y =0和x =0,得
x =3和y =-3.
∴ B(3,0),C(0,-3).
【小题2】(2)∵ 抛物线过点A(-1,0)、B(3,0),
∴ 设抛物线的解析式为:y =a(x+1)(x-3).
∵ 抛物线过点C(0,-3),
∴ -3= a(0+1)(0-3).
∴ a=1.
∴ 抛物线的解析式为:y =(x+1)(x-3). ………………… 4分
即y =x2-2x -3.
【小题3】(3)由y =x2-2x -3,得y =(x -1)2-4.
∴ 抛物线的顶点M(1,-4)
【小题4】(4)如图,存在满足条件的P1(1,-2)和P2(-1,-4).
作MN⊥y轴于点N,则∠CNM=90°.
∵ M(1,-4),C(0,-3),
∴ MN=NC=1.
∴ ∠MCN=45°.
∵∠COB=90°,B(3,0),C(0,-3),
∴ ∠OCB=45°.
∴ ∠BCM=90°. …………………………………………… 6分
∴ 要使点P在直线y =x-3上,必有PC=MC.
∠MPC=∠CMP=45°.
则 过点M分别作x轴和y轴的垂线,交直线y =x -3于点P1和P2.
在y = x -3中,分别令x =1,y =-4,得y =-2,x =-1.
则 P1(1,-2)和P2(-1,-4)
解析


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|查看答案和解析>>
科目:初中数学 来源: 题型:
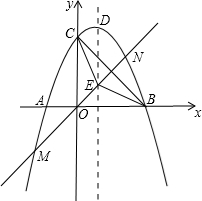 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:
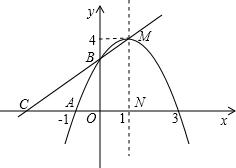 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
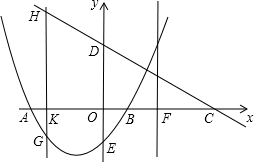 .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.查看答案和解析>>
科目:初中数学 来源: 题型:
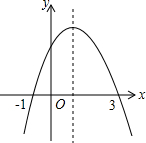 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com