
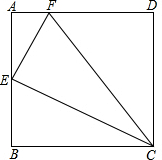
 如图,已知四边形ABCD为正方形,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状,并说明理由.
如图,已知四边形ABCD为正方形,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状,并说明理由. 分析 设AF=a,则FD=3a,DC=BC=4a,AE=EB=2a;在Rt△AEF、Rt△DFC,Rt△EBC中,利用勾股定理求出EF、EC、FC的长,再根据勾股定理的逆定理解答.
解答  解:如图:设AF=a,则FD=3a,DC=BC=4a,AE=EB=2a;
解:如图:设AF=a,则FD=3a,DC=BC=4a,AE=EB=2a;
在Rt△AEF中,EF=$\sqrt{{a}^{2}+(2a)^{2}}$=$\sqrt{5}$a;
在Rt△DFC中,FC=$\sqrt{(3a)^{2}+(4a)^{2}}$=5a;
在Rt△EBC中,EC=$\sqrt{(2a)^{2}+(4a)^{2}}$=2$\sqrt{5}$a.
∴EC2+EF2=FC2,
∴△EFC是直角三角形.
点评 本题考查了勾股定理和勾股定理的逆定理及正方形的性质,利用勾股定理求出三角形三边长,再利用勾股定理逆定理解答,联合运用,是一道好题,值得关注.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 63 | B. | 64 | C. | 65 | D. | 66 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法:
在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com