
 如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )
如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
分析 作A关于CD的对称点A′,连接A′B交CD于P,则点P就是使|PA-PB|的值最大的点,|PA-PB|=A′B,连接A′C,根据等腰直角三角形的性质得到∠CAB=∠ABC=45°,∠ACB=90°,根据三角形的内角和得到∠ACD=75°,于是得到∠CAA′=15°,根据轴对称的性质得到A′C=BC,∠CA′A=∠CAA′=15°,推出△A′BC是腰三角形,根据等边三角形的性质即可得到结论.
解答  解:作A关于CD的对称点A′,连接A′B交CD于P,则点P就是使|PA-PB|的值最大的点,|PA-PB|=A′B,
解:作A关于CD的对称点A′,连接A′B交CD于P,则点P就是使|PA-PB|的值最大的点,|PA-PB|=A′B,
连接A′C,
∵△ABC为等腰直角三角形,AC=BC=4,
∴∠CAB=∠ABC=45°,∠ACB=90°,
∵∠BCD=15°,
∴∠ACD=75°,
∴∠CAA′=15°,
∵AC=A′C,
∴A′C=BC,∠CA′A=∠CAA′=15°,
∴∠ACA′=150°,
∵∠ACB=90°,
∴∠A′CB=60°,
∴△A′BC是等边三角形,
∴A′B=BC=4.
故选A.
点评 此题主要考查轴对称--最短路线问题,等腰直角三角形的性质,等边三角形的判定和性质,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
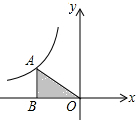 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )| A. | $y=-\frac{2}{x}$ | B. | $y=\frac{2}{x}$ | C. | $y=-\frac{4}{x}$ | D. | $y=\frac{4}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 上周末收盘价 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 10 | +4.5 | -1.5 | +3 | -2.5 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5x2-x2=5 | B. | 4a2+3a2=7a4 | C. | 5+y=5y | D. | -0.25mn+$\frac{1}{4}$mn=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com