
【题目】如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R,S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的序号为( ) 
A.①②③
B.①②④
C.②③④
D.①②③④
【答案】D
【解析】解:∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2﹣PR2 , AS2=AP2﹣PS2 ,
∵AP=AP,PR=PS,
∴AR=AS,∴②正确;
∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,∴③正确;
∵△ABC是等边三角形,
∴∠B=∠CAB=60°,AB=AC,
∵∠QAP=∠BAP,
∴BP=CP,
∵QP∥AB,
∴∠QPC=∠B=60°=∠C,
∴PQ=CQ,
∴△PQC是等边三角形,
∴PQ=CP=BP,∠SQP=60°=∠B,
∵PR⊥AB,PS⊥AC,
∴∠BRP=∠PSQ=90°,
在△BRP和△QSP中,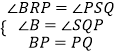 ,
,
∴△BRP≌△QSP,∴④正确;
连接RS,
∵PR=PS,
∴点P在RS的垂直平分线上,
∵AS=AR,
∴点A在RS的垂直平分线上,
∴AP垂直平分RS,∴①正确.
故答案为:①②③④.
根据角平分线性质即可推出②,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP∥AB即可;求出PQ=CP=BP,根据AAS推出△BRP≌△QSP即可,然后根据线段垂直平分线的判定即可得到AP垂直平分RS.


科目:初中数学 来源: 题型:
【题目】春节期间小红和小明进行摸球游戏,在一个不透明的袋子里装有四个球,有3个球上分别写了新、年、好三个不同的字,另一个球上没有写字,游戏规定摸球的人可以任意从口袋中摸出一个球(不再放回),连续摸三回,如摸到新年好三个字则得1分,否则对方得1分.
(1)若由小红摸球,列出树状图或表格求小红获胜的概率;
(2)你认为这个游戏公平吗?如何修改游戏规则才能使该游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东南中学租用两辆小轿车(设速度相同)同时送二名带队老师及![]() 名七年级的学生到育才中学参加数学竞赛,每辆车限坐
名七年级的学生到育才中学参加数学竞赛,每辆车限坐![]() 人(不包括司机).其中一辆小轿车在距离育才中学
人(不包括司机).其中一辆小轿车在距离育才中学![]() 的地方出现故障,此时距离竞赛开始还有
的地方出现故障,此时距离竞赛开始还有![]() 分钟,唯一可利用的交通工具是另一辆小轿车,且这辆车的平均速度是
分钟,唯一可利用的交通工具是另一辆小轿车,且这辆车的平均速度是![]() ,人步行的速度是
,人步行的速度是![]() (上、下车时间忽略不计).
(上、下车时间忽略不计).
(![]() )小李提议:可以让另一辆小轿车先送
)小李提议:可以让另一辆小轿车先送![]() 名学生走,再返回来接我们.你认为小李的提议合理吗?通过计算说明理由.
名学生走,再返回来接我们.你认为小李的提议合理吗?通过计算说明理由.
(![]() )小罗提议:可以让另一辆小车先送
)小罗提议:可以让另一辆小车先送![]() 名学生走,而其它
名学生走,而其它![]() 名师生同时步行前往,小轿车到达考场后再返回途中接送其他人.你认为小罗的提议合理吗?通过计算说明理由.
名师生同时步行前往,小轿车到达考场后再返回途中接送其他人.你认为小罗的提议合理吗?通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=![]() 和y=
和y=![]() 的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为
的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条长为60cm的卷尺铺平后沿着图中箭头的方向折叠,使得卷尺自身的一部分重合,然后在重合部分沿与卷尺的边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度比为1:2:3,则折痕对应的刻度可能的值有 ________.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com