
【题目】根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m2)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题: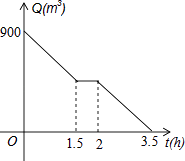
(1)暂停排水需要多少时间?排水孔排水速度是多少?
(2)当2≤t≤3.5时,求Q关于t的函数表达式.
【答案】
(1)解:暂停排水需要的时间为:2﹣1.5=0.5(小时).
∵排水数据为:3.5﹣0.5=3(小时),一共排水900m3,
∴排水孔排水速度是:900÷3=300m3/h
(2)解:当2≤t≤3.5时,设Q关于t的函数表达式为Q=kt+b,易知图象过点(3.5,0).
∵t=1.5时,排水300×1.5=450,此时Q=900﹣450=450,
∴(2,450)在直线Q=kt+b上;
把(2,450),(3.5,0)代入Q=kt+b,
得 ![]() ,解得
,解得 ![]() ,
,
∴Q关于t的函数表达式为Q=﹣300t+1050
【解析】本题考查了一次函数的应用,主要考查学生能否把实际问题转化成数学问题,题目比较典型,是一道比较好的题目.(1)暂停排水时,游泳池内的水量Q保持不变,图象为平行于横轴的一条线段,由此得出暂停排水需要的时间;由图象可知,该游泳池3个小时排水900(m3),根据速度公式求出排水速度即可;(2)当2≤t≤3.5时,设Q关于t的函数表达式为Q=kt+b,易知图象过点(3.5,0),再求出(2,450)在直线y=kt+b上,然后利用待定系数法求出表达式即可.


科目:初中数学 来源: 题型:
【题目】图形变换中的数学,问题情境:在课堂上,兴趣学习小组对一道数学问题进行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连接CD.
(1)探索发现:
如图①,BC与BD的数量关系是;
(2)猜想验证:
如图②,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想BF,BP,BD三者之间的数量关系,并证明你的结论;
(3)拓展延伸:
若点P是线段CB延长线上一动点,按照(2)中的作法,请在图③中补全图象,并直接写出BF、BP、BD三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在三角形ABC中,点O是AC边上的一个动点,过点O做直线MN平行于BC,设MN∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 
(1)试说明:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下面的例题:
解方程:x2﹣|x|﹣2=0.
解:①x≥0时,原方程化为x2﹣x﹣2=0,解得x1=2,x2=﹣1(不合题意,舍去).
②x<0时,原方程化为x2+x﹣2=0,解得x1=﹣2,x2=1(不合题意,舍去).
∴原方程的根是x1=2,x2=﹣2.
请参照例题解方程x2+|x﹣4|﹣8=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书超过200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.
(1)分别求直线l1与x轴,直线l2与AB的交点坐标;
(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)图1中a的值为;
(2)求统计的这组初赛成绩数据的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y= ![]() 交于点C(1,a).
交于点C(1,a).
(1)试确定双曲线的函数表达式;
(2)将l1沿y轴翻折后,得到l2 , 画出l2的图象,并求出l2的函数表达式;
(3)在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程x2﹣3x+p=0(p≠0)的两个不相等的实数根分别为a和b,且a2﹣ab+b2=18,则 ![]() +
+ ![]() 的值是( )
的值是( )
A.3
B.﹣3
C.5
D.﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com