
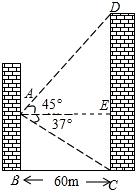
 如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)
如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)分析 首先过点A作AE⊥CD于E,可得四边形ABCE是矩形,即可得BC=AE=60米,然后分别在Rt△ACE中,EC=AE•tan∠EAC与在Rt△ADE中,DE=AE,继而求得大厦的高度.
解答 解:过点A作AE⊥CD于E,
∵AB⊥BC,DC⊥BC,
∴四边形ABCE是矩形,
∵BC=60米,
∴AE=BC=60米,
∴在RT△AEC中,EC=AE•tan∠EAC=60×tan37°≈45.2(米),
在Rt△ADE中,∵∠DAE=45°,
∴DE=AE=60(米),
∴BC=DE+CE=60+45.2=105.2(米).
答:该大厦的高度约为105.2米.
点评 此题考查了仰角与俯角的知识.注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.


科目:初中数学 来源: 题型:解答题
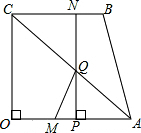 如图,四边形OABC为直角梯形,OA∥BC,∠AOC=90°,OA=OC=4,BC=3.点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动,当其中一个动点达到终点时,另一个动点也随之停止运动,过点N作NP垂直OA于点P,连接AC交NP于点Q,连接MQ.
如图,四边形OABC为直角梯形,OA∥BC,∠AOC=90°,OA=OC=4,BC=3.点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动,当其中一个动点达到终点时,另一个动点也随之停止运动,过点N作NP垂直OA于点P,连接AC交NP于点Q,连接MQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
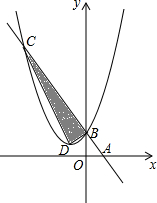 如图,在直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与抛物线相交于点C,则S△ABO:S△BCD=( )
如图,在直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与抛物线相交于点C,则S△ABO:S△BCD=( )| A. | 1:8 | B. | 1:6 | C. | 1:4 | D. | 1:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,我国南海诸岛不断受到外国非法骚扰,为此,我军经常会做针对性海上演习,如图,在一次军事演习中,蓝方在一条东西轴向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
近年来,我国南海诸岛不断受到外国非法骚扰,为此,我军经常会做针对性海上演习,如图,在一次军事演习中,蓝方在一条东西轴向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
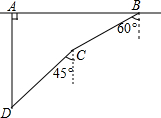
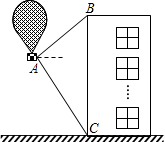 “五一”节期间在我市市民广场进行了热气球飞行表演,如图,有一热气球到达离地面高度为36米的A处时,仪器显示如图,有一热气球到达离地面高度为36米的A处时,仪器显正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
“五一”节期间在我市市民广场进行了热气球飞行表演,如图,有一热气球到达离地面高度为36米的A处时,仪器显示如图,有一热气球到达离地面高度为36米的A处时,仪器显正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
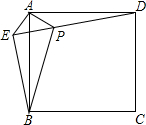 如图,点E是正方形ABCD外一点,连接AE,BE和DE,过点A作AE的垂线交DE于P,若AE=AP=1,PB=3,下列结论:
如图,点E是正方形ABCD外一点,连接AE,BE和DE,过点A作AE的垂线交DE于P,若AE=AP=1,PB=3,下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com