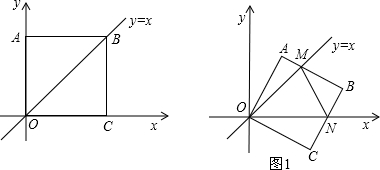
(1)在平面直角坐标系中,将点A(-3,4)向右平移5个单位到点A1,再将点A1绕坐标原点顺时针旋转90°到点A2.直接写出点A1,A2的坐标;
(2)在平面直角坐标系中,将第二象限内的点B(a,b)向右平移m个单位到第一象限点B1,再将点B1绕坐标原点顺时针旋转90°到点B2,直接写出点B1,B2的坐标;
(3)在平面直角坐标系中.将点P(c,d)沿水平方向平移n个单位到点P1,再将点P1绕坐标原点顺时针旋转90°到点P2,直接写出点P2的坐标.
【答案】
分析:(1)如图,由于将点A(-3,4)向右平移5个单位到点A
1,根据平移规律可以得到A
1的坐标,又将点A
1绕坐标原点顺时针旋转90°到点A
2,根据旋转得到△OMA
1≌△OM
1A
2,由此就可以确定A
2的坐标;
(2)可以利用(1)中的规律依次分别得到B
1的坐标,B
2的坐标;
(3)分两种情况:①当把点P(c,d)沿水平方向右平移n个单位到点P
1,此时可以利用(2)的规律求出P
1和P
2的坐标;②当把点P(c,d)沿水平方向左平移n个单位到点P
1,那么P
1的横坐标和前面的计算方法恰好相反,用减法,然后将点P
1绕坐标原点顺时针旋转90°到点P
2的坐标的规律也恰好相反,由此可以直接得到P
2的坐标.
解答:
解:(1)如图,∵将点A(-3,4)向右平移5个单位到点A
1,
∴A
1的坐标为(2,4),
∵又将点A
1绕坐标原点顺时针旋转90°到点A
2,
∴△OMA
1≌△OM
1A
2,
∴A
2的坐标(4,-2).
(2)根据(1)中的规律得:
B
1的坐标为(a+m,b),B
2的坐标为(b,-a-m).
(3)分两种情况:
①当把点P(c,d)沿水平方向右平移n个单位到点P
1,
∴P
1的坐标为(c+n,d),
则P
2的坐标为(d,-c-n);
②当把点P(c,d)沿水平方向左平移n个单位到点P
1,
∴P
1的坐标为(c-n,d),
然后将点P
1绕坐标原点顺时针旋转90°到点P
2,
∴P
2的坐标(d,-c+n).
点评:此题比较复杂,首先要根据具体图形找到图形各点的坐标移动规律,若原来的坐标为(a,b),绕原点顺时针旋转90°后的坐标为(b,-a),然后利用规律就可以求出后面问题的结果.

 解:(1)如图,∵将点A(-3,4)向右平移5个单位到点A1,
解:(1)如图,∵将点A(-3,4)向右平移5个单位到点A1,

 阅读快车系列答案
阅读快车系列答案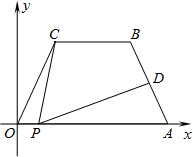 如图所示,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,点P不与点0、点A重合.连接CP,过点P作PD交AB于点D.
如图所示,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,点P不与点0、点A重合.连接CP,过点P作PD交AB于点D.
 如图,在平面直角坐标中,以(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C,
如图,在平面直角坐标中,以(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C,