
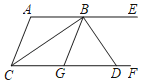
【题目】如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个;④若∠A=α,则∠BDF=![]() .其中正确的有_____.(把你认为正确结论的序号都填上)
.其中正确的有_____.(把你认为正确结论的序号都填上)
【答案】①②④.
【解析】
求出∠EBD+∠ABC=90°,∠DBG+∠CBG=90°,求出∠ABC=∠GBC,根据角平分线的定义即可判断①;根据平行线的性质得出∠ABC=∠BCG,求出∠ACB=∠GBC,根据平行线的判定即可判断②;根据余角的定义即可判断③;根据平行线的性质得出∠EBG=∠A=α,求出∠EBD=![]() ∠EBG=
∠EBG=![]() α,根据平行线的性质得出∠EBD+∠BDF=180°,即可判断④.
α,根据平行线的性质得出∠EBD+∠BDF=180°,即可判断④.
∵BD⊥BC,
∴∠DBC=90°,
∴∠EBD+∠ABC=180°﹣90°=90°,∠DBG+∠CBG=90°,
∵BD平分∠EBG,
∴∠EBD=∠DBG,
∴∠ABC=∠GBC,
即BC平分∠ABG,故①正确;
∵AE∥CF,
∴∠ABC=∠BCG,
∵CB平分∠ACF,
∴∠ACB=∠BCG,
∵∠ABC=∠GBC,
∴∠ACB=∠GBC,
∴AC∥BG,故②正确;
与∠DBE互余的角有∠ABC,∠CBG,∠ACB,∠BCG,共4个,故③错误;
∵AC∥BG,∠A=α,
∴∠EBG=∠A=α,
∵∠EBD=∠DBG,
∴∠EBD=![]() ∠EBG=
∠EBG=![]() ,
,
∵AB∥CF,
∴∠EBD+∠BDF=180°,
∴∠BDF=180°﹣∠EBD=180°﹣![]() ,故④正确;
,故④正确;
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有40m2墙面未来得及粉刷;同样时间内5名二级技工刚好粉刷了10个房间,每名一级技工比二级技工一天多粉刷20m2墙面.
(1)一级技工和二级技工每人每天各粉刷多少墙面?
(2)现有若干间这样的房间需要在规定的时间内粉刷完墙面,若安排一名一级技工单独粉刷,可比规定时间提前1天完成;若安排一名二级技工单独完成,到规定时间还有4间房间没粉刷.需要粉刷的房间一共有多少间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中的一个正方形剪开得到图③,图③中共有7个正方形;将图③中的一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2019个图中共有正方形的个数为( ).
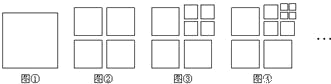
A.6052B.6055C.6058D.6061
查看答案和解析>>
科目:初中数学 来源: 题型:
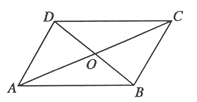
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
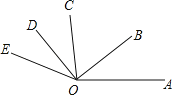
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
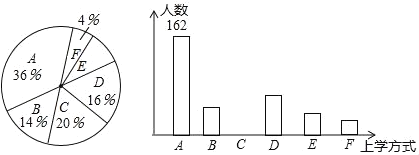
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是平面直角坐标系的原点.在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,1),B(3,1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.设P点运动的时间为t秒(0<t<2).
(1)求经过O、A、B三点的抛物线的解析式;
(2)过P作PD⊥OA于D,以点P为圆心,PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q.
①则P点的坐标为_____,Q点的坐标为_____;(用含t的代数式表示)
②试求t为何值时,⊙P与四边形OABC的两边同时相切;
③设△OPD与四边形OABC重叠的面积为S,请直接写出S与t的函数解析式.
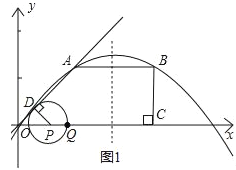
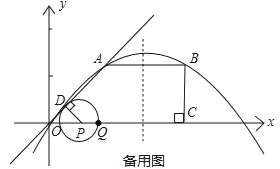
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC=8![]() ,BD=6
,BD=6![]() ,且
,且![]() ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )

A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com