
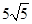 cm,且tan∠EFC=
cm,且tan∠EFC=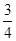 。
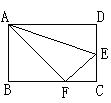
。
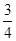
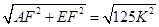 =5
=5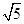


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源:不详 题型:解答题
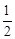 AC的长为半径在AC的两边作弧,交于点M、N;②连接MN,分别交AB、AC于点D、O;③过点C作CE∥AB交MN于点E,连接AE、CD.
AC的长为半径在AC的两边作弧,交于点M、N;②连接MN,分别交AB、AC于点D、O;③过点C作CE∥AB交MN于点E,连接AE、CD.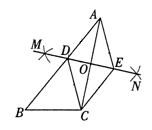
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.三角形的形状不变,三边的比变大 | B.三角形的形状变,三边的比变大 |
| C.三角形的形状变,三边的比不变 | D.三角形的形状不变,三边的比不变 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
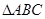 中,
中, ,
, ,
,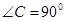 .
.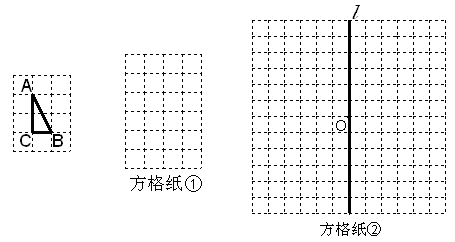
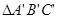 ,使
,使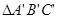 ∽
∽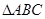 ,且相似比为2︰1;
,且相似比为2︰1;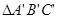 称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点
称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点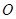 为对称中心,并且以直线
为对称中心,并且以直线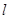 为对称轴的图案.
为对称轴的图案.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
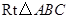 中,
中,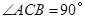 .
.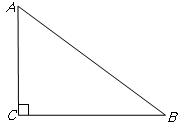
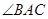 的平分线
的平分线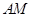 交
交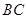 于点
于点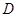 (只保留作图痕迹,不写作法);
(只保留作图痕迹,不写作法);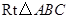 沿某条直线折叠,使点
沿某条直线折叠,使点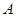 与点
与点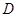 重合,折痕
重合,折痕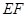 交
交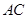 于点
于点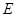 ,交
,交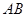 于点
于点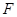 ,连接
,连接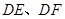 ,再展回到原图形,得到四边形
,再展回到原图形,得到四边形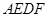 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com